Koren modula x. Modul števila (absolutna vrednost števila), definicije, primeri, lastnosti
V tem članku bomo podrobno analizirali absolutna vrednost števila. Bomo dali različne definicije modul števila, uvesti zapis in grafično ponazoriti. Hkrati si poglejmo različne primere iskanja modula števila po definiciji. Nato bomo našteli in utemeljili glavne lastnosti modula. Na koncu članka bomo govorili o tem, kako se določi in najde modul kompleksnega števila.
Navigacija po straneh.
Številski modul - definicija, zapis in primeri
Najprej se predstavimo oznaka modula števila. Modul števila a bomo zapisali kot , to pomeni, da bomo levo in desno od števila postavili navpične črtice, da tvorimo znak modula. Naj navedemo nekaj primerov. Na primer, modul −7 lahko zapišemo kot ; modul 4.125 je zapisan kot , modul pa ima zapis v obliki .
Naslednja definicija modula se nanaša na , torej na , in na cela števila ter na racionalna in iracionalna števila kot sestavne dele množice realnih števil. Govorili bomo o modulu kompleksnega števila v.
Opredelitev.
Modul števila a– to je bodisi samo število a, če je a pozitivno število, bodisi število −a, nasprotno od števila a, če je a negativno število, ali 0, če je a=0.
Izražena definicija modula števila je pogosto zapisana v naslednji obliki  , ta vnos pomeni, da če a>0 , če a=0 in če a<0
.
, ta vnos pomeni, da če a>0 , če a=0 in če a<0
.
Zapis je mogoče predstaviti v bolj strnjeni obliki  . Ta zapis pomeni, da če je (a večje ali enako 0) in če je a<0
.
. Ta zapis pomeni, da če je (a večje ali enako 0) in če je a<0
.
Obstaja tudi vstop  . Tukaj bi morali posebej pojasniti primer, ko je a=0. V tem primeru imamo , toda −0=0, ker se nič šteje za število, ki je sebi nasprotno.
. Tukaj bi morali posebej pojasniti primer, ko je a=0. V tem primeru imamo , toda −0=0, ker se nič šteje za število, ki je sebi nasprotno.
Dajmo primeri iskanja modula števila z uporabo navedene definicije. Na primer, poiščimo module števil 15 in . Začnimo z iskanjem. Ker je število 15 pozitivno, je njegov modul po definiciji enak temu številu samemu, to je . Kaj je modul števila? Ker je negativno število, je njegov modul enak številu, ki je nasprotno številu, to je številu  . Tako, .
. Tako, .
Za zaključek te točke predstavljamo en sklep, ki je zelo priročen za uporabo v praksi pri iskanju modula števila. Iz definicije modula števila sledi, da modul števila je enak številu pod znakom modula brez upoštevanja njegovega predznaka, in iz zgoraj obravnavanih primerov je to zelo jasno razvidno. Navedena trditev pojasnjuje, zakaj se imenuje tudi modul števila absolutna vrednost števila. Torej modul števila in absolutna vrednostštevilke so eno in isto.
Modul števila kot razdalja
Geometrično si lahko modul števila razlagamo kot razdalja. Dajmo določanje modula števila z razdaljo.
Opredelitev.
Modul števila a– to je razdalja od izhodišča na koordinatni premici do točke, ki ustreza številu a.
Ta definicija je skladna z definicijo modula števila, podano v prvem odstavku. Razjasnimo to točko. Razdalja od izhodišča do točke, ki ustreza pozitivnemu številu, je enaka temu številu. Nič ustreza izhodišču, zato je razdalja od izhodišča do točke s koordinato 0 enaka nič (ni vam treba dati na stran enega segmenta enote in niti enega segmenta, ki sestavlja katerikoli del enotskega segmenta, da bi da pridemo iz točke O v točko s koordinato 0). Razdalja od izhodišča do točke z negativno koordinato je enaka številu, ki je nasprotno koordinati te točke, saj je enaka razdalji od izhodišča do točke, katere koordinata je nasprotno število.
Na primer, modul števila 9 je enak 9, saj je razdalja od izhodišča do točke s koordinato 9 enaka devet. Povejmo še en primer. Točka s koordinato −3,25 se nahaja na razdalji 3,25 od točke O, torej ![]() .
.
Navedena definicija modula števila je poseben primer definicije modula razlike dveh števil.
Opredelitev.
Modul razlike dveh števil a in b je enaka razdalji med točkama koordinatne premice s koordinatama a in b.

To pomeni, da če sta točki na koordinatni premici A(a) in B(b) podani, potem je razdalja od točke A do točke B enaka modulu razlike med številoma a in b. Če vzamemo točko O (izhodišče) kot točko B, potem dobimo definicijo modula števila, podanega na začetku tega odstavka.
Določanje modula števila z uporabo aritmetičnega kvadratnega korena
Občasno se pojavi določanje modula preko aritmetičnega kvadratnega korena.
Izračunajmo na primer module števil −30 in na podlagi te definicije. Imamo. Podobno izračunamo modul dveh tretjin:  .
.
Definicija modula števila skozi aritmetični kvadratni koren je prav tako skladna z definicijo iz prvega odstavka tega člena. Pokažimo ga. Naj bo a pozitivno število in naj bo −a negativno število. Potem ![]() in
in ![]() , če je a=0, potem
, če je a=0, potem ![]() .
.
Lastnosti modula
Modul ima številne značilne rezultate - lastnosti modula. Zdaj bomo predstavili glavne in najpogosteje uporabljene od njih. Pri utemeljevanju teh lastnosti se bomo oprli na definicijo modula števila v smislu razdalje.
Začnimo z najbolj očitno lastnostjo modula - Modul števila ne more biti negativno število. V dobesedni obliki ima ta lastnost obliko za poljubno število a. To lastnost je zelo enostavno utemeljiti: modul števila je razdalja in razdalje ni mogoče izraziti kot negativno število.
Pojdimo na naslednjo lastnost modula. Absolutna vrednost števila enako ničče in samo če je to število nič. Modul nič je po definiciji nič. Nič ustreza izhodišču; nobena druga točka na koordinatni premici ne ustreza ničli, saj je vsako realno število povezano z eno točko na koordinatni premici. Iz istega razloga vsako število, ki ni nič, ustreza točki, ki ni izhodišče. In razdalja od izhodišča do katere koli točke, razen točke O, ni nič, saj je razdalja med dvema točkama nič, če in samo če ti točki sovpadata. Zgornje sklepanje dokazuje, da je samo modul nič enak nič.
Kar daj. Nasprotna števila imajo enake module, to je za poljubno število a. Dejansko sta dve točki na koordinatni premici, katerih koordinate sta nasprotni števili, enako oddaljeni od izhodišča, kar pomeni, da sta modula nasprotnih števil enaka.
Naslednja lastnost modula je: Modul zmnožka dveh števil je enak zmnožku modulov teh števil, to je . Po definiciji je modul produkta števil a in b enak a·b, če , ali −(a·b), če . Iz pravil množenja realnih števil sledi, da je zmnožek modulov števil a in b enak a·b, , ali −(a·b), če je , kar dokazuje obravnavano lastnost.
Modul količnika a, deljenega z b, je enak količniku modula števila, deljenega z modulom b, to je . Utemeljimo to lastnost modula. Ker je količnik enak produktu, potem. Na podlagi prejšnjega premoženja imamo  . Vse kar ostane je, da uporabimo enakost , ki velja na podlagi definicije modula števila.
. Vse kar ostane je, da uporabimo enakost , ki velja na podlagi definicije modula števila.
Naslednja lastnost modula je zapisana kot neenakost: ![]() , a , b in c so poljubna realna števila. Zapisana neenakost ni nič drugega kot neenakost trikotnika. Da bo to jasno, vzemimo točke A(a), B(b), C(c) na koordinatni premici in razmislimo o degeneriranem trikotniku ABC, katerega oglišča ležijo na isti premici. Po definiciji je modul razlike enak dolžini segmenta AB, - dolžini segmenta AC in - dolžini segmenta CB. Ker dolžina katere koli stranice trikotnika ne presega vsote dolžin drugih dveh stranic, potem neenakost velja
, a , b in c so poljubna realna števila. Zapisana neenakost ni nič drugega kot neenakost trikotnika. Da bo to jasno, vzemimo točke A(a), B(b), C(c) na koordinatni premici in razmislimo o degeneriranem trikotniku ABC, katerega oglišča ležijo na isti premici. Po definiciji je modul razlike enak dolžini segmenta AB, - dolžini segmenta AC in - dolžini segmenta CB. Ker dolžina katere koli stranice trikotnika ne presega vsote dolžin drugih dveh stranic, potem neenakost velja ![]() , torej tudi neenakost velja.
, torej tudi neenakost velja.
Pravkar dokazana neenakost je veliko pogostejša v obliki ![]() . Zapisana neenakost se običajno obravnava kot ločena lastnost modula s formulacijo: " Modul vsote dveh števil ne presega vsote modulov teh števil" Toda neenakost sledi neposredno iz neenakosti, če namesto b postavimo −b in vzamemo c=0.
. Zapisana neenakost se običajno obravnava kot ločena lastnost modula s formulacijo: " Modul vsote dveh števil ne presega vsote modulov teh števil" Toda neenakost sledi neposredno iz neenakosti, če namesto b postavimo −b in vzamemo c=0.
Modul kompleksnega števila
Dajmo definicija modula kompleksnega števila. Naj nam bo dano kompleksno število, zapisano v algebraični obliki, kjer sta x in y nekaj realnih števil, ki predstavljata realni in imaginarni del danega kompleksnega števila z, in je imaginarna enota.
Med primerov na modul Pogosto morate najti enačbe korenine modula v modulu, to je enačba oblike
||a*x-b|-c|=k*x+m .
Če je k=0, torej je desna stran enaka konstanti (m), potem je lažje iskati rešitev enačbe z moduli grafično. Spodaj je metoda odpiranje dvojnih modulov z uporabo običajnih primerov v praksi. Dobro razumejte algoritem za izračun enačb z moduli, da ne boste imeli težav pri kvizih, testih in samo na znanje.
Primer 1. Rešite enačbo po modulu |3|x|-5|=-2x-2.
Rešitev: Vedno začnite odpirati enačbe iz notranjega modula
|x|=0 <->x=0.
V točki x=0 se enačba z modulom deli z 2.
Pri x< 0
подмодульная функция отрицательная, поэтому при раскрытии знак меняем на противоположный
|-3x-5|=-2x-2.
Za x>0 ali enako, razširitev modula dobimo
|3x-5|=-2x-2 .
Rešimo enačbo za negativne spremenljivke (x< 0)
. Оно разлагается на две системы уравнений. Первое уравнение получаем из условия, что функция после знака равенства неотрицательна. Второе - раскрывая модуль в одной системе принимаем, что подмодульная функция положительная, в иной отрицательная - меняем знак правой или левой части (зависит от методики преподавания).
Iz prve enačbe dobimo, da rešitev ne sme preseči (-1), tj.
Ta omejitev v celoti sodi v področje, ki ga rešujemo. Premaknimo spremenljivke in konstante na nasprotne strani enakosti v prvem in drugem sistemu
in najti rešitev ![]()
Obe vrednosti pripadata intervalu, ki se obravnava, to je, da sta korenini.
Razmislite o enačbi z moduli za pozitivne spremenljivke
|3x-5|=-2x-2.
Z razširitvijo modula dobimo dva sistema enačb ![]()
Iz prve enačbe, ki je skupna obema sistemoma, dobimo znani pogoj
ki v preseku z množico, na kateri iščemo rešitev, da prazno množico (presečišč ni). Torej so edine korenine modula z modulom vrednosti
x=-3; x=-1,4.
Primer 2. Rešite enačbo z modulom ||x-1|-2|=3x-4.
Rešitev: Začnimo z odpiranjem notranjega modula
|x-1|=0 <=>x=1.
Submodularna funkcija spremeni predznak pri enem. Za manjše vrednosti je negativen, za večje pa pozitiven. V skladu s tem dobimo pri razširitvi notranjega modula dve enačbi z modulom
x |-(x-1)-2|=3x-4;
x>=1 -> |x-1-2|=3x-4.
Ne pozabite preveriti desne strani enačbe modula; ta mora biti večja od nič.
3x-4>=0 -> x>=4/3.
To pomeni, da prve enačbe ni treba reševati, saj je bila zapisana za x< 1,
что не соответствует найденному условию. Раскроем модуль во втором уравнении
|x-3|=3x-4 ->
x-3=3x-4 ali x-3=4-3x;
4-3=3x-x ali x+3x=4+3;
2x=1 ali 4x=7;
x=1/2 ali x=7/4.
Prejeli smo dve vrednosti, od katerih je prva zavrnjena, ker ne spada v zahtevani interval. Končno ima enačba eno rešitev x=7/4.
Primer 3. Rešite enačbo z modulom ||2x-5|-1|=x+3.
Rešitev: Odprimo notranji modul
|2x-5|=0 <=>x=5/2=2,5.
Točka x=2,5 razdeli številsko premico na dva intervala. Oziroma submodularno funkcijo spremeni predznak pri prehodu skozi 2.5. Zapišimo pogoj za rešitev z desna stran enačbe z modulom.
x+3>=0 -> x>=-3.
Torej je rešitev lahko vrednosti, ki niso manjše od (-3) . Razširimo modul za negativno vrednost notranjega modula
|-(2x-5)-1|=x+3;
|-2x+4|=x+3.
Ta modul bo dal tudi 2 enačbi, ko bo razširjen
-2x+4=x+3 ali 2x-4=x+3;
2x+x=4-3 ali 2x-x=3+4;
3x=1; x=1/3 ali x=7.
Vrednost x=7 zavrnemo, saj smo rešitev iskali v intervalu [-3;2,5]. Zdaj odpremo notranji modul za x>2,5. Dobimo enačbo z enim modulom
|2x-5-1|=x+3;
|2x-6|=x+3.
Pri razširitvi modula dobimo naslednje linearne enačbe
-2x+6=x+3 ali 2x-6=x+3;
2x+x=6-3 ali 2x-x=3+6;
3x=3; x=1 ali x=9.
Prva vrednost x=1 ne zadošča pogoju x>2,5. Na tem intervalu imamo torej en koren enačbe z modulom x=9, skupaj pa sta dva (x=1/3).S substitucijo lahko preverite pravilnost izvedenih izračunov
Odgovor: x=1/3; x=9.
Primer 4. Poiščite rešitve za dvojni modul ||3x-1|-5|=2x-3.
Rešitev: Razširimo notranji modul enačbe
|3x-1|=0 <=>x=1/3.
Točka x=2,5 deli številsko premico na dva intervala in dano enačbo na dva primera. Zapišemo pogoj za rešitev glede na obliko enačbe na desni strani
2x-3>=0 -> x>=3/2=1,5.
Iz tega sledi, da nas zanimajo vrednosti >=1,5. torej modularna enačba upoštevajte dva intervala
,
|-(3x-1)-5|=2x-3;
|-3x-4|=2x-3.
Nastali modul, ko je razširjen, je razdeljen na 2 enačbi
-3x-4=2x-3 ali 3x+4=2x-3;
2x+3x=-4+3 ali 3x-2x=-3-4;
5x=-1; x=-1/5 ali x=-7.
Obe vrednosti ne spadata v interval, to pomeni, da nista rešitvi enačbe z moduli. Nato bomo razširili modul za x>2,5. Dobimo naslednjo enačbo
|3x-1-5|=2x-3;
|3x-6|=2x-3.
Z razširitvijo modula dobimo 2 linearni enačbi
3x-6=2x-3 oz –(3x-6)=2x-3;
3x-2x=-3+6 ali 2x+3x=6+3;
x=3 ali 5x=9; x=9/5=1,8.
Druga ugotovljena vrednost ne ustreza pogoju x>2,5, zato jo zavrnemo.
Končno imamo en koren enačbe z moduli x=3.
Izvajanje preverjanja
||3*3-1|-5|=2*3-3 3=3
.
Koren enačbe z modulom je bil pravilno izračunan.
Odgovor: x=1/3; x=9.
Matematike ne izbiramo njen poklic in ona nas izbere.
Ruski matematik Yu.I. Manin
Enačbe z modulom
Najtežje rešljive naloge pri šolski matematiki so enačbe, ki vsebujejo spremenljivke pod znakom modula. Za uspešno reševanje takih enačb morate poznati definicijo in osnovne lastnosti modula. Seveda morajo učenci imeti veščine za reševanje tovrstnih enačb.
Osnovni pojmi in lastnosti
Modul (absolutna vrednost) realnega števila označen z in je opredeljen na naslednji način:
Preproste lastnosti modula vključujejo naslednja razmerja:
Opomba, da zadnji dve lastnosti veljata za vsako sodo stopnjo.
Še več, če, kje, potem in
več kompleksne lastnosti modul, ki jih lahko učinkovito uporabimo pri reševanju enačb z moduli, so formulirani z naslednjimi izreki:
1. izrek.Za vse analitične funkcije in neenakost je res
2. izrek. Enakost je enakovredna neenakosti.
Izrek 3. Enakopravnost enako neenakosti.
Oglejmo si tipične primere reševanja problemov na temo "Enačbe, ki vsebuje spremenljivke pod znakom modula."
Reševanje enačb z modulom
Najpogostejša metoda v šolski matematiki za reševanje enačb z modulom je metoda, temelji na razširitvi modula. Ta metoda je univerzalna, vendar pa lahko v splošnem primeru njegova uporaba vodi do zelo okornih izračunov. V zvezi s tem bi morali učenci poznati dr, več učinkovite metode in tehnike za reševanje takih enačb. Še posebej, potrebno je imeti veščine uporabe izrekov, naveden v tem članku.
Primer 1. Reši enačbo. (1)
rešitev. Enačbo (1) bomo reševali s “klasično” metodo – metodo razkrivanja modulov. Če želite to narediti, razdelimo številsko os pike in na intervale in upoštevajte tri primere.
1. Če , potem , , , in ima enačba (1) obliko . Iz tega izhaja. Vendar tukaj torej ugotovljena vrednost ni koren enačbe (1).
2. Če, potem iz enačbe (1) dobimo ali .
Od takrat koren enačbe (1).
3. Če, potem ima enačba (1) obliko ali . Naj opozorimo, da.
Odgovor: , .
Pri reševanju nadaljnjih enačb z modulom bomo aktivno uporabljali lastnosti modulov za povečanje učinkovitosti reševanja tovrstnih enačb.
Primer 2. Reši enačbo.
rešitev. Ker in potem iz enačbe sledi. V zvezi s tem, , , in enačba dobi obliko. Od tu naprej. Vendar pa zato izvirna enačba nima korenin.
Odgovor: brez korenin.
Primer 3. Reši enačbo.
rešitev. Od takrat. Če, potem in enačba dobi obliko.
Od tu dobimo.
Primer 4. Reši enačbo.
rešitev.Prepišimo enačbo v enakovredni obliki. (2)
Nastala enačba spada med enačbe tipa .
Ob upoštevanju izreka 2 lahko trdimo, da je enačba (2) enakovredna neenakosti . Od tu dobimo.
Odgovor: .
Primer 5. Reši enačbo.
rešitev. Ta enačba ima obliko. Zato , po teoremu 3, tukaj imamo neenakost ali .
Primer 6. Reši enačbo.
rešitev. Predpostavimo, da. Ker , potem ima podana enačba obliko kvadratne enačbe, (3)
Kje . Ker ima enačba (3) en sam pozitivni koren in potem . Od tu dobimo dva korena prvotne enačbe: In .
Primer 7. Reši enačbo. (4)
rešitev. Ker je enačbaje enakovredna kombinaciji dveh enačb: in , potem je pri reševanju enačbe (4) potrebno upoštevati dva primera.
1. Če , potem ali .
Od tu dobimo in .
2. Če , potem ali .
Od takrat.
Odgovor: , , , .
Primer 8.Reši enačbo . (5)
rešitev. Ker in , potem . Od tod in iz enačbe (5) sledi in , tj. tukaj imamo sistem enačb
Vendar je ta sistem enačb nedosleden.
Odgovor: brez korenin.
Primer 9. Reši enačbo. (6)
rešitev.Če označimo , potem in iz enačbe (6) dobimo
ali . (7)
Ker ima enačba (7) obliko , je ta enakovredna neenačbi . Od tu dobimo. Od , torej oz.
Odgovor: .
Primer 10.Reši enačbo. (8)
rešitev.Po teoremu 1 lahko pišemo
(9)
Ob upoštevanju enačbe (8) sklepamo, da obe neenakosti (9) prehajata v enačbe, tj. obstaja sistem enačb
Vendar pa je po izreku 3 zgornji sistem enačb enakovreden sistemu neenačb
(10)
Z reševanjem sistema neenačb (10) dobimo . Ker je sistem neenačb (10) enakovreden enačbi (8), ima izvirna enačba en koren.
Odgovor: .
Primer 11. Reši enačbo. (11)
rešitev. Naj in , potem enakost izhaja iz enačbe (11).
Iz tega sledi in. Tako imamo tukaj sistem neenakosti
Rešitev tega sistema neenakosti je In .
Odgovor: , .
Primer 12.Reši enačbo. (12)
rešitev. Enačbo (12) bomo reševali z metodo zaporedne ekspanzije modulov. Če želite to narediti, razmislimo o več primerih.
1. Če , potem .
1.1. Če , potem in , .
1.2. Če, potem. Vendar pa zato v tem primeru enačba (12) nima korenin.
2. Če , potem .
2.1. Če , potem in , .
2.2. Če , potem in .
Odgovor: , , , , .
Primer 13.Reši enačbo. (13)
rešitev. Ker je leva stran enačbe (13) nenegativna, potem . V zvezi s tem in enačba (13)
dobi obliko oz.
Znano je, da enačba je enakovredna kombinaciji dveh enačb in , rešitev, ki jo dobimo, . Ker , potem ima enačba (13) en koren.
Odgovor: .
Primer 14. Reši sistem enačb (14)
rešitev. Ker in , potem in . Posledično iz sistema enačb (14) dobimo štiri sisteme enačb:
Koreni zgornjih sistemov enačb so koreni sistema enačb (14).
Odgovor: ,, , , , , , .
Primer 15. Reši sistem enačb (15)
rešitev. Od takrat. V zvezi s tem dobimo iz sistema enačb (15) dva sistema enačb
Koreni prvega sistema enačb sta in , iz drugega sistema enačb pa dobimo in .
Odgovor: , , , .
Primer 16. Reši sistem enačb (16)
rešitev. Iz prve enačbe sistema (16) sledi, da .
Od takrat . Oglejmo si drugo enačbo sistema. Zaradi, to , in enačba dobi obliko, ali .
Če zamenjate vrednostv prvo enačbo sistema (16), potem ali .
Odgovor: , .
Za globlji študij metod reševanja problemov, povezanih z reševanjem enačb, ki vsebuje spremenljivke pod znakom modula, Vaje lahko priporočite s seznama priporočene literature.
1. Zbirka nalog iz matematike za kandidate na visokih šolah / Ed. M.I. Scanavi. – M.: Mir in izobraževanje, 2013. – 608 str.
2. Suprun V.P. Matematika za srednješolce: naloge povečane zahtevnosti. – M.: CD “Librocom” / URSS, 2017. – 200 str.
3. Suprun V.P. Matematika za srednješolce: nestandardne metode reševanje problema. – M.: CD “Librocom” / URSS, 2017. – 296 str.
Imate še vprašanja?
Če želite dobiti pomoč mentorja, se registrirajte.
spletne strani, pri kopiranju materiala v celoti ali delno je obvezna povezava do vira.
Modul je absolutna vrednost izraza. Da bi nekako označili modul, je običajno uporabiti ravne oklepaje. Vrednost, ki je v sodih oklepajih, je vrednost, ki je vzeta po modulu. Postopek reševanja katerega koli modula je sestavljen iz odpiranja tistih zelo ravnih oklepajev, ki se v matematičnem jeziku imenujejo modularni oklepaji. Njihovo razkritje poteka v skladu z določenim številom pravil. Tudi v vrstnem redu reševanja modulov najdemo nize vrednosti tistih izrazov, ki so bili v modularnih oklepajih. V večini primerov se modul razširi tako, da izraz, ki je bil podmodularen, prejme pozitivne in negativne vrednosti, vključno z vrednostjo nič. Če izhajamo iz ugotovljenih lastnosti modula, potem se pri tem sestavijo različne enačbe ali neenačbe iz prvotnega izraza, ki jih je nato treba rešiti. Ugotovimo, kako rešiti module.
Postopek rešitve
Reševanje modula se začne s pisanjem izvirne enačbe z modulom. Če želite odgovoriti na vprašanje, kako rešiti enačbe z modulom, ga morate popolnoma odpreti. Za rešitev takšne enačbe se modul razširi. Upoštevati je treba vse modularne izraze. Treba je ugotoviti, pri katerih vrednostih neznanih količin, vključenih v njegovo sestavo, modularni izraz v oklepajih postane nič. Da bi to naredili, je dovolj, da izraz v modularnih oklepajih enačimo z nič in nato izračunamo rešitev dobljene enačbe. Najdene vrednosti je treba zabeležiti. Na enak način morate določiti tudi vrednost vseh neznanih spremenljivk za vse module v tej enačbi. Nato morate začeti definirati in upoštevati vse primere obstoja spremenljivk v izrazih, ko so drugačne od vrednosti nič. Če želite to narediti, morate zapisati nek sistem neenakosti, ki ustreza vsem modulom v prvotni neenakosti. Neenakosti morajo biti sestavljene tako, da zajemajo vse razpoložljive in možne vrednosti za spremenljivko, ki se nahaja na številski premici. Nato morate za vizualizacijo narisati to isto številsko premico, na katero kasneje narišete vse dobljene vrednosti.
Na internetu je zdaj mogoče narediti skoraj vse. Modul ni izjema od pravila. Lahko ga rešite na spletu na enem od številnih sodobnih virov. Vse tiste vrednosti spremenljivke, ki so v ničelnem modulu, bodo posebna omejitev, ki bo uporabljena v procesu reševanja modularne enačbe. V prvotni enačbi morate odpreti vse razpoložljive modularne oklepaje, medtem ko spremenite znak izraza, tako da vrednosti želene spremenljivke sovpadajo s tistimi vrednostmi, ki so vidne na številski premici. Nastalo enačbo je treba rešiti. Vrednost spremenljivke, ki jo bomo pridobili pri reševanju enačbe, je treba preveriti glede na omejitev, ki jo določa sam modul. Če vrednost spremenljivke v celoti izpolnjuje pogoj, potem je pravilna. Vse korenine, ki jih bomo dobili med reševanjem enačbe, vendar ne bodo ustrezale omejitvam, je treba zavreči.
Srednja šola MBOU št. 17, Ivanovo
« Enačbe z modulom"
Metodološki razvoj
Sestavljeno
učiteljica matematike
Lebedeva N.V.20010
Pojasnilo
Poglavje 1. Uvod
Oddelek 2. Osnovne lastnosti Oddelek 3. Geometrična razlaga koncepta modula števila Razdelek 4. Graf funkcije y = |x| Oddelek 5. KonvencijePoglavje 2. Reševanje enačb, ki vsebujejo modul
Razdelek 1. Enačbe oblike |F(x)| = m (najenostavnejši) Razdelek 2. Enačbe oblike F(|x|) = m Razdelek 3. Enačbe oblike |F(x)| = G(x) Razdelek 4. Enačbe oblike |F(x)| = ± F(x) (najlepši) Razdelek 5. Enačbe oblike |F(x)| = |G(x)| Oddelek 6. Primeri reševanja nestandardnih enačb Razdelek 7. Enačbe oblike |F(x)| + |G(x)| = 0 Razdelek 8. Enačbe oblike |a 1 x ± b 1 | ± |a 2 x ± v 2 | ± …|a n x ± in n | = m Oddelek 9. Enačbe, ki vsebujejo več modulovPoglavje 3. Primeri reševanja različnih enačb z modulom.
Oddelek 1. Trigonometrične enačbe Razdelek 2. Eksponentne enačbe Razdelek 3. Logaritemske enačbe Oddelek 4. Iracionalne enačbe Razdelek 5. Napredne naloge Odgovori na vaje BibliografijaPojasnilo.
Koncept absolutne vrednosti (modula) realnega števila je ena njegovih bistvenih značilnosti. Ta koncept je zelo razširjen v različnih delih fizikalnih, matematičnih in tehničnih znanosti. V praksi poučevanja matematičnih predmetov v Srednja šola v skladu s programom Ministrstva za obrambo Ruske federacije se koncept "absolutne vrednosti števila" večkrat srečuje: v 6. razredu se uvaja definicija modula in njegov geometrijski pomen; v 8. razredu se oblikuje koncept absolutne napake, obravnava se rešitev najpreprostejših enačb in neenačb, ki vsebujejo modul, preučujejo se lastnosti aritmetike kvadratni koren; v 11. razredu koncept najdemo v razdelku »Koren n- stopnja." Izkušnje poučevanja kažejo, da se učenci pogosto srečujejo s težavami pri reševanju nalog, ki zahtevajo poznavanje te snovi, in jih pogosto preskočijo, ne da bi jih začeli dokončati. Podobne naloge vsebujejo tudi besedila izpitnih nalog za predmete 9. in 11. razreda. Poleg tega so zahteve, ki jih univerze postavljajo diplomantom, različne, in sicer bolj visoka stopnja kot zahteve šolskega kurikuluma. Za življenje v sodobni družbi je zelo pomembno oblikovanje matematičnega načina razmišljanja, ki se kaže v določenih miselnih veščinah. V procesu reševanja problemov z moduli je potrebna sposobnost uporabe tehnik, kot so generalizacija in specifikacija, analiza, klasifikacija in sistematizacija ter analogija. Reševanje takšnih nalog vam omogoča, da preizkusite svoje znanje o glavnih delih šolskega tečaja, ravni logično razmišljanje, začetne raziskovalne sposobnosti. to delo je namenjen enemu od razdelkov - reševanju enačb, ki vsebujejo modul. Sestavljena je iz treh poglavij. Prvo poglavje predstavlja osnovne koncepte in najpomembnejše teoretične premisleke. Drugo poglavje predlaga devet glavnih vrst enačb, ki vsebujejo modul, razpravlja o metodah za njihovo reševanje in preučuje primere različne ravni težave. Tretje poglavje ponuja kompleksnejše in nestandardne enačbe (trigonometrične, eksponentne, logaritemske in iracionalne). Za vsako vrsto enačb so vaje za samostojno reševanje (odgovori in navodila so priloženi). Glavni namen tega dela je metodološka pomoč učiteljem pri pripravi na pouk in pri organizaciji izbirnih predmetov. Gradivo se lahko uporablja tudi kot učni pripomoček za srednješolce. Naloge, predlagane v delu, so zanimive in jih ni vedno enostavno rešiti, kar omogoča bolj zavestno izobraževalno motivacijo študentov, preverjanje njihovih sposobnosti in povečanje stopnje pripravljenosti diplomantov za vpis na univerze. Diferenciran izbor predlaganih vaj vključuje prehod z reproduktivne ravni obvladovanja gradiva na ustvarjalno, pa tudi priložnost, da se naučite, kako uporabiti svoje znanje pri reševanju nestandardnih problemov.Poglavje 1. Uvod.
Oddelek 1. Določitev absolutne vrednosti .
Opredelitev : Absolutna vrednost (modul) realnega števila A nenegativno število imenujemo: A oz -A. Oznaka: │ A │ Vnos se glasi: “modul števila a” ali “absolutna vrednost števila a”│ a, če je a > 0
│a│ = │ 0, če je a = 0 (1)
│ - in, če aPrimeri: 1) │2,5│ = 2,5 2) │-7│ = 7 3) │1 - √2│ = √2 – 1
- Razširi izrazni modul:
Oddelek 2. Osnovne lastnosti.
Razmislimo o osnovnih lastnostih absolutne vrednosti. Lastnost #1: Nasprotna števila imajo enake module, tj. │а│=│- а│ Pokažimo, da je enakost resnična. Zapišimo definicijo števila - A : │- a│= (2) Primerjajmo niza (1) in (2). Očitno so definicije absolutnih vrednosti števil A in - A ujemati se. torej │а│=│- а│Pri obravnavanju naslednjih lastnosti se bomo omejili na njihovo formulacijo, saj je njihov dokaz podan v Lastnost #2: Absolutna vrednost vsote končnega števila realnih števil ne presega vsote absolutnih vrednosti členov: │а 1 + а 2 +…+ а n │ ≤│а 1 │+│а 2 │ + … + │а n │ Lastnost #3: Absolutna vrednost razlike med dvema realnima številoma ne presega vsote njunih absolutnih vrednosti: │а - в│ ≤│а│+│в│ Lastnost #4: Absolutna vrednost produkta končnega števila realnih števil je enaka produktu absolutnih vrednosti faktorjev: │а·в│=│а│·│в│ Lastnost #5: Absolutna vrednost količnika realnih števil je enaka količniku njihovih absolutnih vrednosti:

Oddelek 3. Geometrična razlaga koncepta modula števila.
Vsakemu realnemu številu lahko pridružimo točko na številski premici, ki bo geometrijska slika tega realnega števila. Vsaka točka na številski premici ustreza svoji oddaljenosti od izhodišča, tj. dolžina odseka od izhodišča do dane točke. Ta razdalja se vedno obravnava kot nenegativna vrednost. Zato bo dolžina ustreznega segmenta geometrijska interpretacija absolutne vrednosti danega realnega števila
Predstavljena geometrijska ilustracija jasno potrjuje lastnost št. 1, tj. modula nasprotnih števil sta enaka. Od tu je enostavno razumljiva veljavnost enakosti: │х – а│= │а – x│. Tudi rešitev enačbe │х│= m, kjer je m ≥ 0, in sicer x 1,2 = ± m, postane bolj očitna. Primeri: 1) │х│= 4 x 1,2 = ± 4 2) │х - 3│= 1
 x 1,2 = 2; 4
x 1,2 = 2; 4 Oddelek 4. Graf funkcije y = │х│
Domena te funkcije so vsa realna števila.Oddelek 5. Konvencije.
V prihodnje bomo pri obravnavi primerov reševanja enačb uporabili naslednje simboli: ( - znak sistema [ - znak celote Pri reševanju sistema enačb (neenačb) se najde presečišče rešitev enačb (neenačb), ki so vključene v sistem. Pri reševanju množice enačb (neenačb) se najde unija rešitev, vključenih v množico enačb (neenačb).Poglavje 2. Reševanje enačb, ki vsebujejo modul.
V tem poglavju si bomo ogledali algebraične metode za reševanje enačb, ki vsebujejo enega ali več modulov.Razdelek 1. Enačbe oblike │F (x)│= m
Enačba te vrste se imenuje najenostavnejša. Ima rešitev, če in samo če je m ≥ 0. Po definiciji modula je izvirna enačba enakovredna nizu dveh enačb: │ F(x)│=m
 Primeri:
Primeri:
№1. Rešite enačbo: │7х - 2│= 9


 Odgovor: x 1
= - 1; X 2
= 1
4
/
7
№2
Odgovor: x 1
= - 1; X 2
= 1
4
/
7
№2
│x 2 + 3x + 1│= 1

 x 2 + 3x + 2 = 0 x 2 +3x = 0 x 1 = -1; x 2 = -2 x (x + 3) = 0 x 1 = 0; x 2 = -3 Odgovor: vsota korenin je - 2.№3
x 2 + 3x + 2 = 0 x 2 +3x = 0 x 1 = -1; x 2 = -2 x (x + 3) = 0 x 1 = 0; x 2 = -3 Odgovor: vsota korenin je - 2.№3
│x 4 -5x 2 + 2│= 2 x 4 – 5x 2 = 0 x 4 – 5x 2 + 4 = 0 x 2 (x 2 – 5) = 0 pomeni x 2 = m, m ≥ 0 x = 0 ; ±√5 m 2 – 5m + 4 = 0 m = 1; 4 – obe vrednosti izpolnjujeta pogoj m ≥ 0 x 2 = 1 x 2 = 4 x = ± 1 x = ± 2 Odgovor: število korenov enačbe 7. vaje:
№1. Rešite enačbo in navedite vsoto korenov: │х - 5│= 3 №2 . Rešite enačbo in označite manjši koren: │x 2 + x│= 0 №3 . Rešite enačbo in označite večji koren: │x 2 – 5x + 4│= 4 №4 .Reši enačbo in označi cel koren: │2x 2 – 7x + 6│= 1 №5 .Rešite enačbo in označite število korenov: │x 4 – 13x 2 + 50│= 14
Oddelek 2. Enačbe oblike F(│х│) = m
Argument funkcije na levi strani je pod znakom modula in desni del ni odvisen od spremenljivke. Razmislimo o dveh načinih reševanja enačb te vrste. 1 način: Po definiciji absolutne vrednosti je prvotna enačba enakovredna kombinaciji dveh sistemov. V vsakem od njih je podmodularnemu izrazu naložen pogoj. F(│х│) =m Ker je funkcija F(│x│) soda v celotnem definicijskem področju, sta korena enačb F(x) = m in F(- x) = m pari nasprotnih števil. Zato je dovolj, da rešimo enega od sistemov (pri obravnavanju primerov na ta način bo podana rešitev enega sistema). 2. način: Uporaba metode uvajanja nove spremenljivke. V tem primeru je uvedena oznaka │x│= a, kjer je a ≥ 0. Ta metoda je zasnovo manj obsežna.
Ker je funkcija F(│x│) soda v celotnem definicijskem področju, sta korena enačb F(x) = m in F(- x) = m pari nasprotnih števil. Zato je dovolj, da rešimo enega od sistemov (pri obravnavanju primerov na ta način bo podana rešitev enega sistema). 2. način: Uporaba metode uvajanja nove spremenljivke. V tem primeru je uvedena oznaka │x│= a, kjer je a ≥ 0. Ta metoda je zasnovo manj obsežna. Primeri: №1 . Rešite enačbo: 3x 2 – 4│x│= - 1 Uporabimo uvedbo nove spremenljivke. Označimo │x│= a, kjer je a ≥ 0. Dobimo enačbo 3a 2 - 4a + 1 = 0 D = 16 – 12 = 4 a 1 = 1 a 2 = 1 / 3 Vrnitev na prvotno spremenljivko: │ x│=1 in │х│= 1/3. Vsaka enačba ima dva korena. Odgovor: x 1 = 1; X 2 = - 1; X 3 = 1 / 3 ; X 4 = - 1 / 3 . №2. Rešite enačbo: 5x 2 + 3│x│- 1 = 1 / 2 │x│ + 3x 2
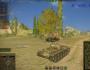
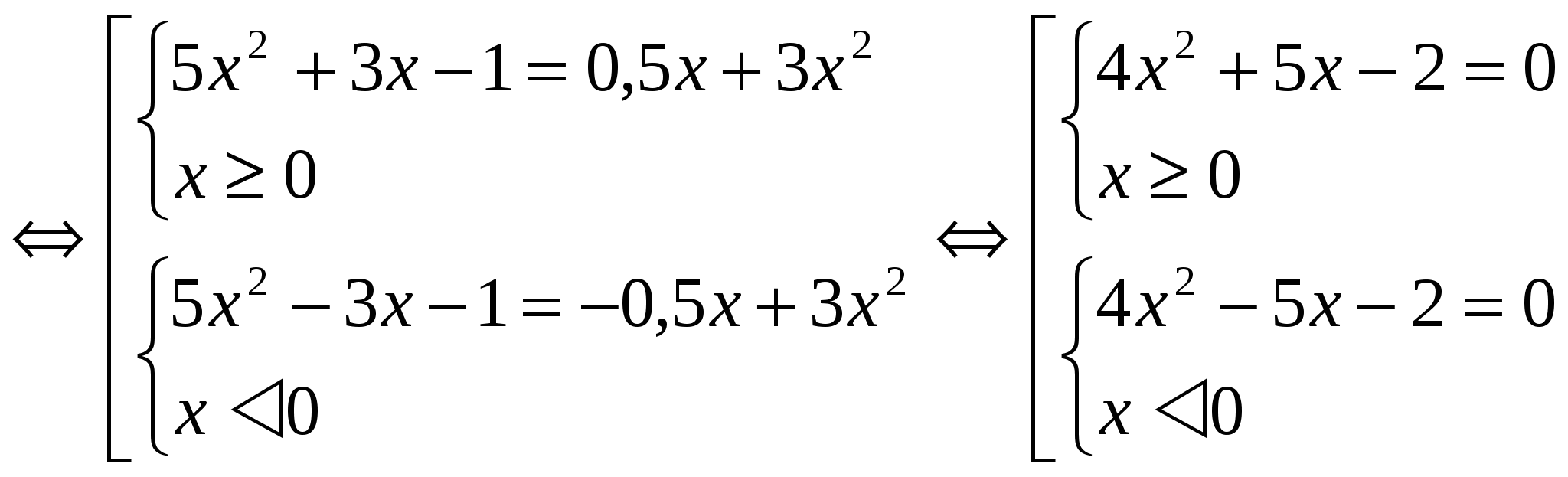 Poiščimo rešitev prvega sistema populacije: 4x 2 + 5x – 2 =0 D = 57 x 1 = -5+√57 / 8 x 2 = -5-√57 / 8 Upoštevajte, da x 2 ne izpolnjuje pogoj x ≥ 0. Rešitev drugi sistem bo število nasprotno od vrednosti x 1. Odgovor: x 1
=
-5+√57
/
8
; X 2
=
5-√57
/
8
.№3
.
Rešimo enačbo: x 4 – │х│= 0 Označimo │х│= a, kjer je a ≥ 0. Dobimo enačbo a 4 – a = 0 a · (a 3 – 1) = 0 a 1 = 0 a 2 = 1 Vrnitev na prvotno spremenljivko: │х│=0 in │х│= 1 x = 0; ± 1 Odgovor: x 1
= 0; X 2
= 1; X 3
= - 1.
Poiščimo rešitev prvega sistema populacije: 4x 2 + 5x – 2 =0 D = 57 x 1 = -5+√57 / 8 x 2 = -5-√57 / 8 Upoštevajte, da x 2 ne izpolnjuje pogoj x ≥ 0. Rešitev drugi sistem bo število nasprotno od vrednosti x 1. Odgovor: x 1
=
-5+√57
/
8
; X 2
=
5-√57
/
8
.№3
.
Rešimo enačbo: x 4 – │х│= 0 Označimo │х│= a, kjer je a ≥ 0. Dobimo enačbo a 4 – a = 0 a · (a 3 – 1) = 0 a 1 = 0 a 2 = 1 Vrnitev na prvotno spremenljivko: │х│=0 in │х│= 1 x = 0; ± 1 Odgovor: x 1
= 0; X 2
= 1; X 3
= - 1.
vaje: №6. Rešite enačbo: 2│х│ - 4,5 = 5 – 3 / 8 │х│ №7 . Rešite enačbo, v odgovoru navedite število korenov: 3x 2 - 7│x│ + 2 = 0 №8 . Rešite enačbo, v odgovoru navedite celoštevilske rešitve: x 4 + │x│ - 2 = 0
Razdelek 3. Enačbe oblike │F(x)│ = G(x)
Desna stran enačbe te vrste je odvisna od spremenljivke in ima zato rešitev, če in samo če je desna stran funkcija G(x) ≥ 0. Prvotno enačbo je mogoče rešiti na dva načina : 1 način: Standard, ki temelji na razkritju modula na podlagi njegove definicije in je sestavljen iz enakovrednega prehoda na kombinacijo dveh sistemov. │ F(x)│ =G(X)
 To metodo je smiselno uporabiti v primeru kompleksnega izraza za funkcijo G(x) in manj kompleksnega za funkcijo F(x), saj se predpostavlja, da bodo rešene neenačbe s funkcijo F(x). 2. način: Sestavljen je iz prehoda na enakovredni sistem, v katerem je na desni strani naložen pogoj. │ F(x)│=
G(x)
To metodo je smiselno uporabiti v primeru kompleksnega izraza za funkcijo G(x) in manj kompleksnega za funkcijo F(x), saj se predpostavlja, da bodo rešene neenačbe s funkcijo F(x). 2. način: Sestavljen je iz prehoda na enakovredni sistem, v katerem je na desni strani naložen pogoj. │ F(x)│=
G(x)

 Ta metoda je primernejša za uporabo, če je izraz za funkcijo G(x) manj kompleksen kot za funkcijo F(x), saj je predpostavljena rešitev neenačbe G(x) ≥ 0. Poleg tega je v primeru več modulov, je priporočljivo uporabiti drugo možnost. Primeri:
№1.
Rešite enačbo: │x + 2│= 6 -2x
Ta metoda je primernejša za uporabo, če je izraz za funkcijo G(x) manj kompleksen kot za funkcijo F(x), saj je predpostavljena rešitev neenačbe G(x) ≥ 0. Poleg tega je v primeru več modulov, je priporočljivo uporabiti drugo možnost. Primeri:
№1.
Rešite enačbo: │x + 2│= 6 -2x  (1 način) Odgovor: x = 1 1
/
3
№2.
(1 način) Odgovor: x = 1 1
/
3
№2.
│х 2 – 2х - 1│= 2·(x + 1)
 (2 način) Odgovor: Produkt korenin je 3.
(2 način) Odgovor: Produkt korenin je 3.№3. Rešite enačbo in v odgovoru navedite vsoto korenin:
│x - 6│= x 2 - 5x + 9

Odgovor: vsota korenin je 4.
vaje: №9. │x + 4│= - 3x №10. Rešite enačbo, navedite število rešitev v odgovoru:│x 2 + x - 1│= 2x – 1 №11 . Rešite enačbo, v odgovoru označite zmnožek korenov:│x + 3│= x 2 + x – 6
Razdelek 4. Enačbe oblike │F(x)│= F(x) in │F(x)│= - F(x)
Enačbe te vrste se včasih imenujejo "najlepše". Ker je desna stran enačb odvisna od spremenljivke, obstajajo rešitve, če in samo če je desna stran nenegativna. Zato so izvirne enačbe enakovredne neenačbam:│F(x)│= F(x) F(x) ≥ 0 in │F(x)│= - F(x) F(x) Primeri: №1 . Rešite enačbo, v odgovoru označite manjši cel koren: │5x - 3│= 5x – 3 5x – 3 ≥ 0 5x ≥ 3 x ≥ 0,6 Odgovor: x = 1№2. Rešite enačbo, v odgovoru navedite dolžino intervala: │х 2 - 9│= 9 – x 2 x 2 – 9 ≤ 0 (x – 3) (x + 3) ≤ 0 [- 3; 3] Odgovor: dolžina vrzeli je 6.№3 . Rešite enačbo in navedite število celih rešitev v vašem odgovoru: │2 + x – x 2 │= 2 + x – x 2 2 + x – x 2 ≥ 0 x 2 – x – 2 ≤ 0 [- 1; 2] Odgovor: 4 celotne rešitve.№4 . Rešite enačbo in v odgovoru označite največji koren:
│4 – x -
 │= 4 – x –
│= 4 – x –  x 2 – 5x + 5 = 0 D = 5 x 1,2 =
x 2 – 5x + 5 = 0 D = 5 x 1,2 =  ≈ 1,4
≈ 1,4Odgovor: x = 3.
vaje:
№12.
Rešite enačbo, v odgovoru označite cel koren: │x 2 + 6x + 8│= x 2 + 6x + 8 №13.
Rešite enačbo, v odgovoru navedite število celih rešitev: │13x – x 2 - 36│+ x 2 – 13x + 36 = 0 №14.
Rešite enačbo; v odgovoru označite celo število, ki ni koren enačbe: 
Razdelek 5. Enačbe oblike │F(x)│= │G(x)│
Ker sta obe strani enačbe nenegativni, rešitev vključuje upoštevanje dveh primerov: submodularni izrazi so enakega ali nasprotnega predznaka. Zato je prvotna enačba enakovredna kombinaciji dveh enačb: │ F(x)│= │ G(x)│ Primeri:
№1.
Rešite enačbo, v odgovoru navedite cel koren: │x + 3│=│2x - 1│
Primeri:
№1.
Rešite enačbo, v odgovoru navedite cel koren: │x + 3│=│2x - 1│  Odgovor: cel koren x = 4.№2.
Reši enačbo: │
x – x 2 - 1│=│2x – 3 – x 2 │
Odgovor: cel koren x = 4.№2.
Reši enačbo: │
x – x 2 - 1│=│2x – 3 – x 2 │  Odgovor: x = 2.№3
.
Rešite enačbo in v odgovoru označite produkt korenin:
Odgovor: x = 2.№3
.
Rešite enačbo in v odgovoru označite produkt korenin: 


 Korenske enačbe 4x 2 + 2x – 1 = 0 x 1,2 = - 1±√5 / 4 Odgovor: produkt korenin je – 0,25. vaje:
№15
. Rešite enačbo in v odgovoru navedite celotno rešitev: │x 2 – 3x + 2│= │x 2 + 6x - 1│ №16.
Rešite enačbo, v odgovoru označite manjši koren:│5x - 3│=│7 - x│ №17
. Rešite enačbo in v odgovoru navedite vsoto korenin:
Korenske enačbe 4x 2 + 2x – 1 = 0 x 1,2 = - 1±√5 / 4 Odgovor: produkt korenin je – 0,25. vaje:
№15
. Rešite enačbo in v odgovoru navedite celotno rešitev: │x 2 – 3x + 2│= │x 2 + 6x - 1│ №16.
Rešite enačbo, v odgovoru označite manjši koren:│5x - 3│=│7 - x│ №17
. Rešite enačbo in v odgovoru navedite vsoto korenin: 
Oddelek 6. Primeri reševanja nestandardnih enačb
V tem razdelku si bomo ogledali primere nestandardnih enačb, pri reševanju katerih se absolutna vrednost izraza razkrije z definicijo. Primeri:№1.
Rešite enačbo, v odgovoru navedite vsoto korenov: x · │x│- 5x – 6 = 0  Odgovor: vsota korenin je 1 №2.
.
Rešite enačbo, v odgovoru označite manjši koren: x 2 - 4x ·
Odgovor: vsota korenin je 1 №2.
.
Rešite enačbo, v odgovoru označite manjši koren: x 2 - 4x ·  - 5 = 0
- 5 = 0  Odgovor: manjši koren x = - 5. №3.
Reši enačbo:
Odgovor: manjši koren x = - 5. №3.
Reši enačbo:  Odgovor: x = -1. vaje:
№18.
Rešite enačbo in označite vsoto korenov: x · │3x + 5│= 3x 2 + 4x + 3
Odgovor: x = -1. vaje:
№18.
Rešite enačbo in označite vsoto korenov: x · │3x + 5│= 3x 2 + 4x + 3
№19.
Reši enačbo: x 2 – 3x = 
№20.
Reši enačbo: 
Razdelek 7. Enačbe oblike │F(x)│+│G(x)│=0
Lahko opazimo, da je na levi strani enačbe te vrste vsota nenegativnih količin. Zato ima izvirna enačba rešitev, če in samo če sta oba člena enaka nič hkrati. Enačba je enakovredna sistemu enačb: │ F(x)│+│ G(x)│=0 Primeri:
№1
. Reši enačbo:
Primeri:
№1
. Reši enačbo:  Odgovor: x = 2. №2.
Reši enačbo: Odgovor: x = 1. vaje:
№21.
Reši enačbo: №22
. Rešite enačbo in v odgovoru navedite vsoto korenin: №23
. Rešite enačbo in v odgovoru označite število rešitev:
Odgovor: x = 2. №2.
Reši enačbo: Odgovor: x = 1. vaje:
№21.
Reši enačbo: №22
. Rešite enačbo in v odgovoru navedite vsoto korenin: №23
. Rešite enačbo in v odgovoru označite število rešitev: Oddelek 8. Enačbe oblike │a 1 x + b 1 │±│a 2 x + b 2 │± … │a n x +b n │= m
Za reševanje tovrstnih enačb se uporablja intervalna metoda. Če jo rešimo z zaporedno širitvijo modulov, dobimo n sklopov sistemov, kar je zelo okorno in neprijetno. Oglejmo si algoritem intervalne metode: 1). Poiščite vrednosti spremenljivk X, pri katerem je vsak modul enak nič (ničle submodularnih izrazov): 2). Najdene vrednosti označite na številski premici, ki je razdeljena na intervale (število intervalov je enako n+1
) 3). Ugotovite, s kakšnim znakom je vsak modul razkrit v vsakem od dobljenih intervalov (pri reševanju lahko uporabite številsko premico in na njej označite znake) 4). Prvotna enačba je enakovredna agregatu n+1
sistemov, v vsakem od katerih je navedena pripadnost spremenljivke X enega od intervalov. Primeri:
№1
. Rešite enačbo in v odgovoru označite največji koren:
2). Najdene vrednosti označite na številski premici, ki je razdeljena na intervale (število intervalov je enako n+1
) 3). Ugotovite, s kakšnim znakom je vsak modul razkrit v vsakem od dobljenih intervalov (pri reševanju lahko uporabite številsko premico in na njej označite znake) 4). Prvotna enačba je enakovredna agregatu n+1
sistemov, v vsakem od katerih je navedena pripadnost spremenljivke X enega od intervalov. Primeri:
№1
. Rešite enačbo in v odgovoru označite največji koren:  1). Poiščimo ničle submodularnih izrazov: x = 2; x = -3 2). Označimo najdene vrednosti na številski premici in določimo, s kakšnim znakom je vsak modul razkrit na nastalih intervalih:
1). Poiščimo ničle submodularnih izrazov: x = 2; x = -3 2). Označimo najdene vrednosti na številski premici in določimo, s kakšnim znakom je vsak modul razkrit na nastalih intervalih: x – 2 x – 2 x – 2 - - + - 3 2 x 2x + 6 2x + 6 2x + 6 - + + 3)
 - ni rešitev Enačba ima dva korena. Odgovor: največji koren x = 2. №2.
Rešite enačbo in v svoj odgovor vnesite celoten koren:
- ni rešitev Enačba ima dva korena. Odgovor: največji koren x = 2. №2.
Rešite enačbo in v svoj odgovor vnesite celoten koren:  1). Poiščimo ničle submodularnih izrazov: x = 1,5; x = - 1 2). Označimo najdene vrednosti na številski premici in določimo, s kakšnim znakom je vsak modul razkrit na dobljenih intervalih: x + 1 x + 1 x + 1 - + +
1). Poiščimo ničle submodularnih izrazov: x = 1,5; x = - 1 2). Označimo najdene vrednosti na številski premici in določimo, s kakšnim znakom je vsak modul razkrit na dobljenih intervalih: x + 1 x + 1 x + 1 - + + -1 1,5 x 2x – 3 2x – 3 2x – 3 - - +
3).
 Zadnji sistem nima rešitev, zato ima enačba dva korena. Pri reševanju enačbe bodite pozorni na znak »-« pred drugim modulom. Odgovor: cel koren x = 7. №3.
Rešite enačbo, v odgovoru navedite vsoto korenov: 1). Poiščimo ničle submodularnih izrazov: x = 5; x = 1; x = - 2 2). Označimo najdene vrednosti na številski premici in določimo, s kakšnim znakom je vsak modul razkrit v nastalih intervalih: x – 5 x – 5 x – 5 x – 5 - - - +
Zadnji sistem nima rešitev, zato ima enačba dva korena. Pri reševanju enačbe bodite pozorni na znak »-« pred drugim modulom. Odgovor: cel koren x = 7. №3.
Rešite enačbo, v odgovoru navedite vsoto korenov: 1). Poiščimo ničle submodularnih izrazov: x = 5; x = 1; x = - 2 2). Označimo najdene vrednosti na številski premici in določimo, s kakšnim znakom je vsak modul razkrit v nastalih intervalih: x – 5 x – 5 x – 5 x – 5 - - - + -2 1 5 x x – 1 x – 1 x – 1 x – 1 - - + + x + 2 x + 2 x + 2 x + 2 - + + +
3).
 Enačba ima dva korena x = 0 in 2. Odgovor: vsota korenin je 2. №4
.
Reši enačbo: 1). Poiščimo ničle submodularnih izrazov: x = 1; x = 2; x = 3. 2). Ugotovimo, s kakšnim predznakom je vsak modul razkrit na dobljenih intervalih. 3).
Enačba ima dva korena x = 0 in 2. Odgovor: vsota korenin je 2. №4
.
Reši enačbo: 1). Poiščimo ničle submodularnih izrazov: x = 1; x = 2; x = 3. 2). Ugotovimo, s kakšnim predznakom je vsak modul razkrit na dobljenih intervalih. 3).  Združimo rešitve prvih treh sistemov. Odgovor: ; x = 5.
Združimo rešitve prvih treh sistemov. Odgovor: ; x = 5.vaje: №24. Reši enačbo:
 №25.
Rešite enačbo in v odgovoru navedite vsoto korenin: №26.
Rešite enačbo in v odgovoru označite manjši koren: №27.
Rešite enačbo in v odgovoru označite večji koren:
№25.
Rešite enačbo in v odgovoru navedite vsoto korenin: №26.
Rešite enačbo in v odgovoru označite manjši koren: №27.
Rešite enačbo in v odgovoru označite večji koren: Oddelek 9. Enačbe, ki vsebujejo več modulov
Enačbe, ki vsebujejo več modulov, predvidevajo prisotnost absolutnih vrednosti v submodularnih izrazih. Osnovno načelo za reševanje enačb te vrste je zaporedno razkritje modulov, začenši z "zunanjim". Med reševanjem se uporabljajo tehnike, obravnavane v razdelkih št. 1, št. 3.Primeri:
№1.
Reši enačbo:  Odgovor: x = 1; - enajst. №2.
Reši enačbo:
Odgovor: x = 1; - enajst. №2.
Reši enačbo:
Odgovor: x = 0; 4; - 4. №3.
Rešite enačbo in v odgovoru označite produkt korenin:  Odgovor: produkt korenin je – 8. №4.
Reši enačbo:
Odgovor: produkt korenin je – 8. №4.
Reši enačbo:  Označimo enačbe populacije (1)
in (2)
in razmislite o rešitvi za vsako od njih posebej zaradi lažjega načrtovanja. Ker obe enačbi vsebujeta več kot en modul, je primerneje izvesti enakovreden prehod na množice sistemov. (1)
Označimo enačbe populacije (1)
in (2)
in razmislite o rešitvi za vsako od njih posebej zaradi lažjega načrtovanja. Ker obe enačbi vsebujeta več kot en modul, je primerneje izvesti enakovreden prehod na množice sistemov. (1)

 (2)
(2)


 odgovor:
odgovor:
vaje:
№36.
Rešite enačbo, v odgovoru navedite vsoto korenov: 5 │3x-5│ = 25 x №37.
Rešite enačbo, če je korenin več, v odgovoru navedite vsoto korenin: │x + 2│ x – 3x – 10 = 1 №38.
Rešite enačbo: 3 │2х -4│ = 9 │х│ №39.
Rešite enačbo in v odgovoru navedite število korenov: 2 │ sin x│ = √2 №40
. Rešite enačbo in v odgovoru navedite število korenin:
Oddelek 3. Logaritemske enačbe.
Preden rešimo naslednje enačbe, je potrebno pregledati lastnosti logaritmov in logaritemske funkcije. Primeri: №1. Rešite enačbo, v odgovoru navedite zmnožek korenov: log 2 (x+1) 2 + log 2 │x+1│ = 6 O.D.Z. x+1≠0 x≠ - 1Primer 1: če je x ≥ - 1, potem je log 2 (x+1) 2 + log 2 (x+1) = 6 log 2 (x+1) 3 = log 2 2 6 (x+1) 3 = 2 6 x+1 = 4 x = 3 – izpolnjuje pogoj x ≥ - 1 2 primer: če je x log 2 (x+1) 2 + log 2 (-x-1) = 6 log 2 (x+1) 2 + log 2 (-(x+1)) = 6 log 2 (-(x+1) 3) = log 2 2 6- (x+1) 3 = 2 6- (x+1) = 4 x = - 5 – izpolnjuje pogoj x - 1
Odgovor: produkt korenin je – 15.
№2.
Rešite enačbo, v odgovoru navedite vsoto korenin: lg  O.D.Z.
O.D.Z. 



Odgovor: vsota korenin je 0,5.
№3.
Reši enačbo: log 5  O.D.Z.
O.D.Z. 
 Odgovor: x = 9. №4.
Rešite enačbo: │2 + log 0,2 x│+ 3 = │1 + log 5 x│ O.D.Z. x > 0 Uporabimo formulo za premik na drugo bazo. │2 - log 5 x│+ 3 = │1 + log 5 x│
Odgovor: x = 9. №4.
Rešite enačbo: │2 + log 0,2 x│+ 3 = │1 + log 5 x│ O.D.Z. x > 0 Uporabimo formulo za premik na drugo bazo. │2 - log 5 x│+ 3 = │1 + log 5 x│
│2 - log 5 x│- │1 + log 5 x│= - 3 Poiščemo ničle submodularnih izrazov: x = 25; x = Te številke razdelijo obseg sprejemljivih vrednosti v tri intervale, tako da je enačba enakovredna nizu treh sistemov.  odgovor:)
odgovor:)