Modül x'in kökü. Bir sayının modülü (bir sayının mutlak değeri), tanımlar, örnekler, özellikler
Bu yazıda detaylı olarak analiz edeceğiz bir sayının mutlak değeri. Vereceğiz çeşitli tanımlar Bir sayının modülü, notasyonu tanıtın ve grafik illüstrasyonlar sağlayın. Aynı zamanda, bir sayının modülünü tanım gereği bulmanın çeşitli örneklerine bakalım. Bundan sonra modülün ana özelliklerini listeleyip gerekçelendireceğiz. Yazının sonunda bir karmaşık sayının modülünün nasıl belirlenip bulunduğundan bahsedeceğiz.
Sayfada gezinme.
Sayı modülü - tanım, gösterim ve örnekler
İlk önce tanıtıyoruz sayı modülü tanımı. a sayısının modülünü yazacağız yani sayının soluna ve sağına modül işaretini oluşturacak şekilde dikey çizgiler koyacağız. Birkaç örnek verelim. Örneğin modül −7 şu şekilde yazılabilir; modül 4.125 olarak yazılır ve modül formun gösterimine sahiptir.
Aşağıdaki modül tanımı, gerçek sayılar kümesinin kurucu parçaları olarak ve dolayısıyla tamsayılara ve rasyonel ve irrasyonel sayılara atıfta bulunur. Karmaşık bir sayının modülü hakkında konuşacağız.
Tanım.
a sayısının modülü– a pozitif bir sayıysa bu, a sayısının kendisidir veya a negatif bir sayıysa a sayısının tersi olan −a sayısıdır veya a=0 ise 0'dır.
Bir sayının modülünün sesli tanımı genellikle aşağıdaki biçimde yazılır  , bu giriş şu anlama gelir: if a>0 , if a=0 ve if a<0
.
, bu giriş şu anlama gelir: if a>0 , if a=0 ve if a<0
.
Kayıt daha kompakt bir biçimde sunulabilir  . Bu gösterim şu anlama gelir: if (a, 0'dan büyük veya ona eşit) ve if a<0
.
. Bu gösterim şu anlama gelir: if (a, 0'dan büyük veya ona eşit) ve if a<0
.
Giriş de var  . Burada a=0 durumunu ayrıca açıklamamız gerekir. Bu durumda elimizde −0=0 vardır, çünkü sıfır kendinin karşıtı olan bir sayı olarak kabul edilir.
. Burada a=0 durumunu ayrıca açıklamamız gerekir. Bu durumda elimizde −0=0 vardır, çünkü sıfır kendinin karşıtı olan bir sayı olarak kabul edilir.
Hadi verelim bir sayının modülünü bulma örnekleri Belirtilen bir tanımı kullanarak. Örnek olarak 15 ve 15 sayılarının modüllerini bulalım. Bulmakla başlayalım. 15 sayısı pozitif olduğu için modülü tanım gereği bu sayının kendisine eşittir, yani. Bir sayının modülü nedir? Negatif bir sayı olduğu için modülü sayının karşısındaki sayıya yani sayıya eşittir.  . Böylece, .
. Böylece, .
Bu noktayı sonuçlandırmak için, bir sayının modülünü bulurken pratikte kullanılabilecek çok uygun bir sonuç sunuyoruz. Bir sayının modülünün tanımından şu sonuç çıkar: bir sayının modülü, işareti dikkate alınmaksızın modül işaretinin altındaki sayıya eşittir Yukarıda tartışılan örneklerden bu çok açık bir şekilde görülmektedir. Belirtilen ifade, bir sayının modülünün neden aynı zamanda çağrıldığını da açıklamaktadır. sayının mutlak değeri. Yani sayının modülü ve mutlak değer sayılar aynı şeydir.
Bir sayının mesafe olarak modülü
Geometrik olarak bir sayının modülü şu şekilde yorumlanabilir: mesafe. Hadi verelim bir sayının modülünün mesafeye göre belirlenmesi.
Tanım.
a sayısının modülü– bu, koordinat çizgisi üzerindeki başlangıç noktasından a sayısına karşılık gelen noktaya kadar olan mesafedir.
Bu tanım, birinci paragrafta verilen bir sayının modül tanımıyla tutarlıdır. Bu noktaya açıklık getirelim. Orijinden pozitif bir sayıya karşılık gelen noktaya olan mesafe bu sayıya eşittir. Sıfır, orijine karşılık gelir, dolayısıyla orijinden 0 koordinatlı noktaya olan mesafe sıfıra eşittir (sırayla tek bir birim segmenti ayırmanıza veya bir birim segmentin herhangi bir kısmını oluşturan tek bir segmenti ayırmanıza gerek yoktur) O noktasından koordinatı 0 olan bir noktaya gitmek için). Orijinden negatif koordinatlı bir noktaya olan uzaklık, bu noktanın koordinatının karşısındaki sayıya eşittir, çünkü orijinden koordinatı karşıt sayı olan noktaya olan mesafeye eşittir.
Örneğin 9 sayısının modülü 9'a eşittir çünkü orijinden 9 koordinatlı noktaya olan mesafe dokuza eşittir. Başka bir örnek verelim. Koordinatı −3,25 olan nokta O noktasından 3,25 uzaklıkta bulunmaktadır, dolayısıyla ![]() .
.
Bir sayının modülünün belirtilen tanımı, iki sayının farkının modülünün tanımının özel bir durumudur.
Tanım.
İki sayının farkının modülü a ve b, koordinat çizgisinin a ve b koordinatlarına sahip noktaları arasındaki mesafeye eşittir.

Yani, A(a) ve B(b) koordinat doğrusu üzerinde noktalar verilmişse, A noktasından B noktasına olan uzaklık, a ve b sayıları arasındaki farkın modülüne eşittir. O noktasını (başlangıç) B noktası olarak alırsak, bu paragrafın başında verilen bir sayının modülünün tanımını elde ederiz.
Aritmetik karekökü kullanarak bir sayının modülünü belirleme
Bazen meydana gelir aritmetik karekök yoluyla modülün belirlenmesi.
Örneğin -30 sayılarının modüllerini bu tanıma göre hesaplayalım. Sahibiz. Benzer şekilde üçte ikisinin modülünü hesaplıyoruz:  .
.
Bir sayının modülünün aritmetik karekök yoluyla tanımı da bu makalenin ilk paragrafında verilen tanımla tutarlıdır. Hadi gösterelim. a pozitif bir sayı olsun ve -a negatif bir sayı olsun. Daha sonra ![]() Ve
Ve ![]() , eğer a=0 ise, o zaman
, eğer a=0 ise, o zaman ![]() .
.
Modül özellikleri
Modülün bir dizi karakteristik sonucu vardır - modül özellikleri. Şimdi bunlardan başlıcalarını ve en sık kullanılanlarını sunacağız. Bu özellikleri gerekçelendirirken, bir sayının modülünün uzaklık cinsinden tanımına güveneceğiz.
Modülün en belirgin özelliğiyle başlayalım: Bir sayının modülü negatif bir sayı olamaz. Kelimenin tam anlamıyla bu özellik herhangi bir a sayısı biçimine sahiptir. Bu özelliğin gerekçelendirilmesi çok kolaydır: Bir sayının modülü bir mesafedir ve mesafe negatif bir sayı olarak ifade edilemez.
Bir sonraki modül özelliğine geçelim. Bir sayının mutlak değeri sıfıra eşit ancak ve ancak bu sayı sıfırsa. Sıfırın modülü tanım gereği sıfırdır. Sıfır orijine karşılık gelir; her gerçek sayı koordinat çizgisi üzerinde tek bir noktayla ilişkili olduğundan koordinat çizgisi üzerindeki başka hiçbir nokta sıfıra karşılık gelmez. Aynı sebepten dolayı sıfırdan farklı herhangi bir sayı, orijinden farklı bir noktaya karşılık gelir. Ve başlangıç noktasından O noktası dışındaki herhangi bir noktaya olan mesafe sıfır değildir, çünkü iki nokta arasındaki mesafe ancak ve ancak bu noktalar çakışırsa sıfırdır. Yukarıdaki mantık, yalnızca sıfır modülünün sıfıra eşit olduğunu kanıtlar.
Devam etmek. Karşıt sayıların eşit modülleri vardır, yani herhangi bir sayı için a. Nitekim koordinat doğrusu üzerinde koordinatları zıt sayılar olan iki nokta orijinden aynı uzaklıkta bulunmaktadır, yani zıt sayıların modülleri eşittir.
Modülün aşağıdaki özelliği: İki sayının çarpımının modülü bu sayıların modüllerinin çarpımına eşittir, yani, . Tanım gereği, a ve b sayılarının çarpımının modülü ya a·b'ye ya da eğer −(a·b)'ye eşittir. Gerçel sayıların çarpım kurallarından, a ve b sayılarının modüllerinin çarpımının a·b, veya -(a·b) if'e eşit olduğu sonucu çıkar ve bu da söz konusu özelliği kanıtlar.
a'nın b'ye bölümünün modülü, bir sayının modülünün b'nin modülüne bölümüne eşittir, yani, . Modülün bu özelliğini gerekçelendirelim. Bölüm ürüne eşit olduğundan, o zaman. Sahip olduğumuz önceki mülk sayesinde  . Geriye kalan tek şey, bir sayının modülünün tanımı nedeniyle geçerli olan eşitliği kullanmaktır.
. Geriye kalan tek şey, bir sayının modülünün tanımı nedeniyle geçerli olan eşitliği kullanmaktır.
Bir modülün aşağıdaki özelliği eşitsizlik olarak yazılır: ![]() , a , b ve c keyfi gerçek sayılardır. Yazılı eşitsizlik bundan başka bir şey değil üçgen eşitsizliği. Bunu açıklığa kavuşturmak için koordinat doğrusu üzerinde A(a), B(b), C(c) noktalarını alalım ve köşeleri aynı doğru üzerinde olan dejenere bir ABC üçgenini ele alalım. Tanım gereği, farkın modülü AB parçasının uzunluğuna, - AC parçasının uzunluğuna ve - CB parçasının uzunluğuna eşittir. Bir üçgenin herhangi bir kenarının uzunluğu diğer iki kenarın uzunluklarının toplamını aşmadığından eşitsizlik doğrudur
, a , b ve c keyfi gerçek sayılardır. Yazılı eşitsizlik bundan başka bir şey değil üçgen eşitsizliği. Bunu açıklığa kavuşturmak için koordinat doğrusu üzerinde A(a), B(b), C(c) noktalarını alalım ve köşeleri aynı doğru üzerinde olan dejenere bir ABC üçgenini ele alalım. Tanım gereği, farkın modülü AB parçasının uzunluğuna, - AC parçasının uzunluğuna ve - CB parçasının uzunluğuna eşittir. Bir üçgenin herhangi bir kenarının uzunluğu diğer iki kenarın uzunluklarının toplamını aşmadığından eşitsizlik doğrudur ![]() dolayısıyla eşitsizlik de doğrudur.
dolayısıyla eşitsizlik de doğrudur.
Az önce kanıtlanan eşitsizlik şu biçimde çok daha yaygındır: ![]() . Yazılı eşitsizlik genellikle aşağıdaki formülasyonla modülün ayrı bir özelliği olarak kabul edilir: “ İki sayının toplamının modülü, bu sayıların modüllerinin toplamını aşmaz" Ancak b yerine -b koyarsak ve c=0 alırsak eşitsizlik doğrudan eşitsizlikten kaynaklanır.
. Yazılı eşitsizlik genellikle aşağıdaki formülasyonla modülün ayrı bir özelliği olarak kabul edilir: “ İki sayının toplamının modülü, bu sayıların modüllerinin toplamını aşmaz" Ancak b yerine -b koyarsak ve c=0 alırsak eşitsizlik doğrudan eşitsizlikten kaynaklanır.
Karmaşık bir sayının modülü
Hadi verelim karmaşık bir sayının modülünün tanımı. Bize verilsin karmaşık sayı cebirsel biçimde yazılmıştır; burada x ve y, belirli bir z karmaşık sayısının sırasıyla gerçek ve sanal kısımlarını temsil eden bazı gerçek sayılardır ve sanal birimdir.
Arasında modül başına örnekler Genellikle bulmanız gereken denklemler vardır Bir modüldeki modül kökleri yani formun bir denklemi
||a*x-b|-c|=k*x+m .
Eğer k=0 yani sağ taraf bir sabite (m) eşitse çözüm aramak daha kolay olur Modüllerle denklemleri grafiksel olarak. Yöntem aşağıdadır çift modüllerin açılması pratikte yaygın olan örneklerin kullanılması. Modüllerle denklem hesaplama algoritmasını iyi anlayın, böylece sınavlarda, testlerde sorun yaşamaz ve sadece bilgi sahibi olursunuz.
Örnek 1. Modülo |3|x|-5|=-2x-2 denklemini çözün.
Çözüm: Denklemleri açmaya her zaman dahili modülden başlayın
|x|=0 <->x=0.
x=0 noktasında modüllü denklem 2'ye bölünür.
x'te< 0
подмодульная функция отрицательная, поэтому при раскрытии знак меняем на противоположный
|-3x-5|=-2x-2.
X>0 veya eşit için, elde ettiğimiz modülü genişleterek
|3x-5|=-2x-2 .
Denklemi çözelim negatif değişkenler için (x< 0)
. Оно разлагается на две системы уравнений. Первое уравнение получаем из условия, что функция после знака равенства неотрицательна. Второе - раскрывая модуль в одной системе принимаем, что подмодульная функция положительная, в иной отрицательная - меняем знак правой или левой части (зависит от методики преподавания).
İlk denklemden çözümün (-1)'i aşmaması gerektiğini anlıyoruz;
Bu sınırlama tamamen çözdüğümüz alana aittir. Birinci ve ikinci sistemlerde değişkenleri ve sabitleri eşitliğin karşıt taraflarına taşıyalım
ve bir çözüm bul ![]()
Her iki değer de dikkate alınan aralığa aittir, yani köklerdir.
Pozitif değişkenler için modülleri olan bir denklem düşünün
|3x-5|=-2x-2.
Modülü genişleterek iki denklem sistemi elde ederiz ![]()
İki sistem için ortak olan ilk denklemden tanıdık koşulu elde ederiz.
üzerinde çözüm aradığımız kümeyle kesiştiğinde boş bir küme verir (kesişme noktası yoktur). Yani bir modüle sahip bir modülün tek kökleri değerlerdir
x=-3; x=-1,4.
Örnek 2. Denklemi ||x-1|-2|=3x-4 modülüyle çözün.
Çözüm: Dahili modülü açarak başlayalım
|x-1|=0 <=>x=1.
Bir alt modüler fonksiyon bir noktada işaret değiştirir. Daha küçük değerler için negatif, daha büyük değerler için ise pozitiftir. Buna göre iç modülü genişlettiğimizde modül ile iki denklem elde ederiz.
x |-(x-1)-2|=3x-4;
x>=1 -> |x-1-2|=3x-4.
Modül denkleminin sağ tarafını kontrol ettiğinizden emin olun; sıfırdan büyük olmalıdır.
3x-4>=0 -> x>=4/3.
Bu, x için yazıldığı için ilk denklemi çözmeye gerek olmadığı anlamına gelir.< 1,
что не соответствует найденному условию. Раскроем модуль во втором уравнении
|x-3|=3x-4 ->
x-3=3x-4 veya x-3=4-3x;
4-3=3x-x veya x+3x=4+3;
2x=1 veya 4x=7;
x=1/2 veya x=7/4.
İki değer aldık, bunlardan ilki gerekli aralığa ait olmadığı için reddedildi. Son olarak denklemin bir çözümü var x=7/4.
Örnek 3. Denklemi ||2x-5|-1|=x+3 modülüyle çözün.
Çözüm: Dahili modülü açalım
|2x-5|=0 <=>x=5/2=2,5.
X=2,5 noktası sayı doğrusunu iki aralığa böler. Sırasıyla, alt modüler fonksiyon 2.5'ten geçerken işaret değiştirir. Çözümün koşulunu yazalım. Sağ Taraf modüllü denklemler.
x+3>=0 -> x>=-3.
Yani çözüm (-3)'ten küçük olmayan değerler olabilir. Dahili modülün negatif değeri için modülü genişletelim
|-(2x-5)-1|=x+3;
|-2x+4|=x+3.
Bu modül genişletildiğinde ayrıca 2 denklem verecektir
-2x+4=x+3 veya 2x-4=x+3;
2x+x=4-3 veya 2x-x=3+4;
3x=1; x=1/3 veya x=7 .
[-3;2.5] aralığında bir çözüm aradığımız için x=7 değerini reddediyoruz. Şimdi x>2.5 için dahili modülü açıyoruz. Tek modüllü bir denklem elde ediyoruz
|2x-5-1|=x+3;
|2x-6|=x+3.
Modülü genişletirken aşağıdakileri elde ederiz doğrusal denklemler
-2x+6=x+3 veya 2x-6=x+3;
2x+x=6-3 veya 2x-x=3+6;
3x=3; x=1 veya x=9 .
İlk x=1 değeri x>2,5 koşulunu karşılamamaktadır. Yani bu aralıkta denklemin modül x=9 olan bir kökü var ve toplamda iki tane var (x=1/3).İkame yaparak yapılan hesaplamaların doğruluğunu kontrol edebilirsiniz.
Cevap: x=1/3; x=9.
Örnek 4. Çift modülün çözümlerini bulun ||3x-1|-5|=2x-3.
Çözüm: Denklemin iç modülünü genişletelim.
|3x-1|=0 <=>x=1/3.
X=2,5 noktası sayı doğrusunu iki aralığa, verilen denklemi ise iki duruma bölmektedir. Sağ taraftaki denklemin formuna göre çözümün koşulunu yazıyoruz
2x-3>=0 -> x>=3/2=1,5.
Buradan >=1,5 değerleri ile ilgilendiğimiz anlaşılmaktadır. Böylece modüler denklem iki aralıkta düşünün
,
|-(3x-1)-5|=2x-3;
|-3x-4|=2x-3.
Ortaya çıkan modül genişletildiğinde 2 denkleme bölünür
-3x-4=2x-3 veya 3x+4=2x-3;
2x+3x=-4+3 veya 3x-2x=-3-4;
5x=-1; x=-1/5 veya x=-7 .
Her iki değer de aralığa girmez, yani modüllü denklemin çözümleri değildir. Daha sonra modülü x>2,5 olacak şekilde genişleteceğiz. Aşağıdaki denklemi elde ederiz
|3x-1-5|=2x-3;
|3x-6|=2x-3.
Modülü genişleterek 2 doğrusal denklem elde ederiz
3x-6=2x-3 veya –(3x-6)=2x-3;
3x-2x=-3+6 veya 2x+3x=6+3;
x=3 veya 5x=9; x=9/5=1,8.
Bulunan ikinci değer x>2,5 koşuluna uymuyor, reddediyoruz.
Son olarak modülü x=3 olan denklemin bir köküne sahibiz.
Kontrol gerçekleştirme
||3*3-1|-5|=2*3-3 3=3
.
Modüllü denklemin kökü doğru hesaplandı.
Cevap: x=1/3; x=9.
Biz matematiği seçmiyoruz mesleği ve bizi seçiyor.
Rus matematikçi Yu.I. Manin
Modüllü denklemler
Okul matematiğinde çözülmesi en zor problemler, modül işareti altındaki değişkenleri içeren denklemlerdir. Bu tür denklemleri başarılı bir şekilde çözmek için modülün tanımını ve temel özelliklerini bilmeniz gerekir. Doğal olarak öğrencilerin bu tür denklemleri çözme becerisine sahip olmaları gerekir.
Temel kavramlar ve özellikler
Gerçek bir sayının modülü (mutlak değeri) ile gösterilir ve aşağıdaki gibi tanımlanır:
Bir modülün basit özellikleri aşağıdaki ilişkileri içerir:
Not, son iki özelliğin herhangi bir çift derece için geçerli olduğu.
Üstelik eğer, nerede, o zaman ve
Daha karmaşık özellikler modül, modüllü denklemleri çözerken etkili bir şekilde kullanılabilir, aşağıdaki teoremlerle formüle edilir:
Teorem 1.Herhangi bir analitik fonksiyon için Ve eşitsizlik doğrudur
Teorem 2. Eşitlik eşitsizliğe eşdeğerdir.
Teorem 3. Eşitlik eşitsizlikle eşdeğer.
“Denklemler” konusundaki tipik problem çözme örneklerine bakalım, modül işareti altında değişkenler içeren."
Modüllü denklem çözme
Modüllü denklemleri çözmek için okul matematiğinde en yaygın yöntem, yöntemdir., Modül genişletmeye dayalı. Bu yöntem evrenseldir, ancak genel durumda kullanımı çok zahmetli hesaplamalara yol açabilir. Bu konuda öğrencilerin diğerlerini bilmesi gerekir., Daha etkili yöntemler ve bu tür denklemleri çözme teknikleri. Özellikle, teoremleri uygulama becerisine sahip olmak gerekir, bu makalede verilmiştir.
Örnek 1. Denklemi çözün. (1)
Çözüm. Denklem (1)'i “klasik” yöntem olan modülleri açma yöntemini kullanarak çözeceğiz. Bunu yapmak için sayı eksenini bölelim noktalar ve aralıklara bölün ve üç durumu düşünün.
1. Eğer , , , ve denklem (1) formunu alır. Bundan şu sonuç çıkıyor. Ancak burada dolayısıyla bulunan değer denklemin (1) kökü değildir.
2. Eğer, daha sonra denklem (1)'den elde ederiz veya .
O zamandan beri denklemin kökü (1).
3. Eğer, o zaman denklem (1) şu formu alır veya . Şunu not edelim.
Cevap: , .
Bir modül ile sonraki denklemleri çözerken, bu tür denklemlerin çözüm verimliliğini artırmak için modüllerin özelliklerini aktif olarak kullanacağız.
Örnek 2. Denklemi çözün.
Çözüm. O zamandan beri ve o zaman aşağıdaki denklemden. Bu konuda, , , ve denklem şu şekli alır. Buradan anlıyoruz. Fakat , dolayısıyla orijinal denklemin kökleri yoktur.
Cevap: Kök yok.
Örnek 3. Denklemi çözün.
Çözüm. O zamandan beri. Eğer öyleyse ve denklem şu şekli alır.
Buradan anlıyoruz.
Örnek 4. Denklemi çözün.
Çözüm.Denklemi eşdeğer formda yeniden yazalım. (2)
Ortaya çıkan denklem tipindeki denklemlere aittir.
Teorem 2 dikkate alındığında denklem (2)'nin eşitsizliğe eşdeğer olduğu ileri sürülebilir. Buradan anlıyoruz.
Cevap: .
Örnek 5. Denklemi çözün.
Çözüm. Bu denklem şu şekle sahiptir:. Bu yüzden , Teorem 3'e göre, burada eşitsizlik var veya .
Örnek 6. Denklemi çözün.
Çözüm. Bunu varsayalım. Çünkü , o zaman verilen denklem ikinci dereceden bir denklem şeklini alır, (3)
Nerede . Denklemin (3) tek bir pozitif kökü olduğundan ve daha sonra . Buradan orijinal denklemin iki kökünü elde ederiz: Ve .
Örnek 7. Denklemi çözün. (4)
Çözüm. Denklemden bu yanaiki denklemin birleşimine eşdeğerdir: Ve , o zaman denklem (4)'ü çözerken iki durumu dikkate almak gerekir.
1. Eğer ise veya .
Buradan, ve'yi alıyoruz.
2. Eğer , o zaman veya .
O zamandan beri.
Cevap: , , , .
Örnek 8.Denklemi çözün . (5)
Çözüm. O zamandan beri ve , o zaman . Buradan ve denklem (5)'ten şunu takip eder ve , yani. burada bir denklem sistemimiz var
Ancak bu denklem sistemi tutarsızdır.
Cevap: Kök yok.
Örnek 9. Denklemi çözün. (6)
Çözüm. Eğer belirtirsek, o zaman ve denklem (6)'dan şunu elde ederiz:
Veya . (7)
Denklem (7) şeklinde olduğundan bu denklem eşitsizliğe eşdeğerdir. Buradan anlıyoruz. O zamandan beri veya .
Cevap: .
Örnek 10.Denklemi çözün. (8)
Çözüm.Teorem 1'e göre şunu yazabiliriz:
(9)
Denklem (8) dikkate alındığında, her iki eşitsizliğin de (9) eşitliğe dönüştüğü sonucuna varıyoruz; bir denklem sistemi var
Ancak Teorem 3'e göre yukarıdaki denklem sistemi eşitsizlikler sistemine eşdeğerdir.
(10)
Eşitsizlik sistemini (10) çözerek elde ederiz. Eşitsizlik sistemi (10), denklem (8)'e eşdeğer olduğundan orijinal denklemin tek kökü vardır.
Cevap: .
Örnek 11. Denklemi çözün. (11)
Çözüm. ve olsun, o zaman eşitlik denklem (11)'den gelir.
Bunu takip eder ve . Böylece burada bir eşitsizlik sistemimiz var
Bu eşitsizlik sisteminin çözümü Ve .
Cevap: , .
Örnek 12.Denklemi çözün. (12)
Çözüm. Denklem (12) modüllerin sıralı genişletilmesi yöntemiyle çözülecektir. Bunu yapmak için birkaç durumu ele alalım.
1. Eğer öyleyse .
1.1. Eğer , o zaman ve , .
1.2. Eğer öyleyse. Fakat , dolayısıyla bu durumda denklem (12)'nin kökleri yoktur.
2. Eğer öyleyse .
2.1. Eğer , o zaman ve , .
2.2. Eğer , o zaman ve .
Cevap: , , , , .
Örnek 13.Denklemi çözün. (13)
Çözüm. Denklemin (13) sol tarafı negatif olmadığından, o zaman . Bu bağlamda ve denklem (13)
veya şeklini alır.
Denklemin olduğu biliniyor iki denklemin birleşimine eşdeğerdir Ve , elde ettiğimiz çözümü çözüyoruz, . Çünkü , o zaman denklem (13)'ün bir kökü vardır.
Cevap: .
Örnek 14. Denklem sistemini çözme (14)
Çözüm. O zamandan beri ve , o zaman ve . Sonuç olarak, denklem sisteminden (14) dört denklem sistemi elde ederiz:
Yukarıdaki denklem sistemlerinin kökleri denklem sisteminin (14) kökleridir.
Cevap: ,, , , , , , .
Örnek 15. Denklem sistemini çözme (15)
Çözüm. O zamandan beri. Bu bağlamda, denklem sisteminden (15) iki denklem sistemi elde ediyoruz
Birinci denklem sisteminin kökleri ve'dir ve ikinci denklem sisteminden ve'yi elde ederiz.
Cevap: , , , .
Örnek 16. Denklem sistemini çözme (16)
Çözüm. Sistemin (16) ilk denkleminden şu çıkar.
O zamandan beri . Sistemin ikinci denklemini ele alalım. Çünkü, O , ve denklem şu şekli alır, , veya .
Değeri değiştirirsenizsistemin ilk denklemine (16), sonra , veya .
Cevap: , .
Problem çözme yöntemlerinin daha derinlemesine incelenmesi için, denklem çözmeyle ilgili, modül işaretinin altındaki değişkenleri içeren, Önerilen literatür listesinden öğreticiler önerebilirsiniz.
1. Üniversitelere başvuranlar için matematik problemlerinin toplanması / Ed. Mİ. Scanavi. – M.: Barış ve Eğitim, 2013. – 608 s.
2. V.P.'yi iptal edin. Lise öğrencileri için matematik: artan karmaşıklığın görevleri. – M.: CD “Librocom” / URSS, 2017. – 200 s.
3. V.P.'yi iptal edin. Lise öğrencileri için matematik: standart dışı yöntemler problem çözme. – M.: CD “Librocom” / URSS, 2017. – 296 s.
Hala sorularınız mı var?
Bir öğretmenden yardım almak için kaydolun.
web sitesi, materyalin tamamını veya bir kısmını kopyalarken kaynağa bir bağlantı gereklidir.
Modül, ifadenin mutlak değeridir. Bir modülü bir şekilde belirtmek için düz parantezlerin kullanılması gelenekseldir. Çift parantez içindeki değer modulo olarak alınan değerdir. Herhangi bir modülü çözme süreci, matematik dilinde modüler parantez olarak adlandırılan çok düz parantezlerin açılmasından oluşur. Açıklanmaları belirli sayıda kurala göre gerçekleşir. Ayrıca modüllerin çözüm sırasına göre modüler parantez içindeki ifadelerin değer kümeleri bulunur. Çoğu durumda modül, alt modüler ifadenin sıfır değeri de dahil olmak üzere hem pozitif hem de negatif değerler alacağı şekilde genişletilir. Modülün belirlenmiş özelliklerinden başlarsak, süreçte orijinal ifadeden çeşitli denklemler veya eşitsizlikler derlenir ve bunların daha sonra çözülmesi gerekir. Modüllerin nasıl çözüleceğini bulalım.
Çözüm süreci
Bir modülün çözümü, orijinal denklemin modülle yazılmasıyla başlar. Modüllü denklemlerin nasıl çözüleceği sorusunu cevaplamak için onu tamamen açmanız gerekir. Böyle bir denklemi çözmek için modül genişletilir. Tüm modüler ifadeler dikkate alınmalıdır. Bileşiminde yer alan bilinmeyen miktarların hangi değerlerinde parantez içindeki modüler ifadenin sıfır olacağını belirlemek gerekir. Bunu yapabilmek için modüler parantez içindeki ifadeyi sıfıra eşitlemek ve ardından ortaya çıkan denklemin çözümünü hesaplamak yeterlidir. Bulunan değerlerin kaydedilmesi gerekmektedir. Aynı şekilde bu denklemdeki tüm modüller için tüm bilinmeyen değişkenlerin değerini de belirlemeniz gerekiyor. Daha sonra, sıfır değerinden farklı olduklarında ifadelerdeki değişkenlerin varlığının tüm durumlarını tanımlamaya ve dikkate almaya başlamanız gerekir. Bunu yapmak için orijinal eşitsizliğin tüm modüllerine karşılık gelen bazı eşitsizlik sistemlerini yazmanız gerekir. Eşitsizlikler mevcut tüm eşitsizlikleri kapsayacak şekilde düzenlenmelidir. olası değerler sayı doğrusunda bulunan bir değişken için. Daha sonra görselleştirme için aynı sayı doğrusunu çizmeniz gerekir; daha sonra elde edilen tüm değerlerin üzerine çizilir.
Artık neredeyse her şey internet üzerinden yapılabiliyor. Modül kuralın bir istisnası değildir. Bunu birçok modern kaynaktan birini kullanarak çevrimiçi olarak çözebilirsiniz. Sıfır modülünde bulunan değişkenin tüm bu değerleri, modüler denklemin çözümü sürecinde kullanılacak özel bir kısıtlama olacaktır. Orijinal denklemde, ifadenin işaretini değiştirirken mevcut tüm modüler parantezleri açmanız gerekir, böylece istenen değişkenin değerleri sayı doğrusunda görünen değerlerle çakışır. Ortaya çıkan denklemin çözülmesi gerekir. Denklemin çözümü sırasında elde edilecek değişkenin değeri, modülün kendisi tarafından belirlenen sınırlamaya göre kontrol edilmelidir. Değişkenin değeri koşulu tam olarak sağlıyorsa doğrudur. Denklemin çözümü sırasında elde edilecek ancak kısıtlamalara uymayan tüm köklerin atılması gerekir.
MBOU Ortaokulu No. 17, İvanovo
« Modüllü denklemler"
Metodolojik gelişim
Derlenmiş
Matematik öğretmeni
Lebedeva N.V.20010
Açıklayıcı not
Bölüm 1. Giriş
Bölüm 2. Temel özellikler Bölüm 3. Bir sayının modülü kavramının geometrik yorumu Bölüm 4. y = |x| fonksiyonunun grafiği Bölüm 5. SözleşmelerBölüm 2. Modül içeren denklemlerin çözülmesi
Bölüm 1. |F(x)| formundaki denklemler = m (en basit) Bölüm 2. F(|x|) = m formundaki denklemler Bölüm 3. |F(x)| formundaki denklemler = G(x) Bölüm 4. |F(x)| formundaki denklemler = ± F(x) (en güzel) Bölüm 5. |F(x)| formundaki denklemler = |G(x)| Bölüm 6. Standart olmayan denklemlerin çözümüne örnekler Bölüm 7. |F(x)| formundaki denklemler + |G(x)| = 0 Bölüm 8. |a 1 x ± b 1 | formundaki denklemler ± |a 2 x ± 2'de | ± …|a n x ± inç n | = m Bölüm 9. Birkaç modül içeren denklemlerBölüm 3. Modüllü çeşitli denklemlerin çözümüne örnekler.
Bölüm 1. Trigonometrik denklemler Bölüm 2. Üstel denklemler Bölüm 3. Logaritmik Denklemler Bölüm 4. İrrasyonel denklemler Bölüm 5. Gelişmiş görevler Alıştırmaların cevapları KaynakçaAçıklayıcı not.
Gerçel sayının mutlak değeri (modülü) kavramı onun temel özelliklerinden biridir. Bu kavram fiziksel, matematiksel ve teknik bilimlerin çeşitli bölümlerinde yaygındır. Matematik derslerinin öğretimi uygulamasında lise Rusya Federasyonu Savunma Bakanlığı Programı uyarınca “sayıların mutlak değeri” kavramıyla defalarca karşılaşılmaktadır: 6. sınıfta modülün tanımı ve geometrik anlamı tanıtılmaktadır; 8. sınıfta mutlak hata kavramı oluşturulur, en basit denklemlerin ve modül içeren eşitsizliklerin çözümü dikkate alınır, aritmetiğin özellikleri incelenir kare kök; 11. sınıfta kavram “Kök” bölümünde yer almaktadır. N-inci derece."Öğretim deneyimi, öğrencilerin bu materyal hakkında bilgi gerektiren görevleri çözmede sıklıkla zorluklarla karşılaştıklarını ve çoğu zaman bunları tamamlamaya başlamadan atladıklarını göstermektedir. 9. ve 11. sınıf derslerinin sınav ödev metinleri de benzer ödevleri içermektedir. Ayrıca üniversitelerin okul mezunlarına yüklediği gereksinimler de farklılık göstermektedir. yüksek seviye okul müfredatının gereklerinden daha fazlası. Modern toplumdaki yaşam için, belirli zihinsel becerilerde kendini gösteren matematiksel bir düşünme tarzının oluşumu çok önemlidir. Modüllerle problem çözme sürecinde genelleme ve belirleme, analiz, sınıflandırma ve sistemleştirme, analoji gibi teknikleri kullanma becerisi gereklidir. Bu tür görevleri çözmek, okul kursunun ana bölümleri, seviye hakkındaki bilginizi test etmenize olanak tanır. mantıksal düşünme, ilk araştırma becerileri. bu iş Bir modül içeren denklemlerin çözülmesi bölümlerinden birine ayrılmıştır. Üç bölümden oluşmaktadır. Birinci bölümde temel kavramlar ve en önemli teorik hususlar tanıtılmaktadır. İkinci bölümde bir modül içeren dokuz ana denklem türü öneriliyor, bunları çözme yöntemleri tartışılıyor ve örnekler inceleniyor farklı seviyeler zorluklar. Üçüncü bölümde daha karmaşık ve standart dışı denklemler (trigonometrik, üstel, logaritmik ve irrasyonel) sunulmaktadır. Her denklem türü için bağımsız olarak çözmeye yönelik alıştırmalar vardır (cevaplar ve talimatlar ektedir). Bu çalışmanın temel amacı öğretmenlere derslere hazırlanma ve seçmeli dersleri düzenleme konusunda metodolojik yardım sağlamaktır. Materyal aynı zamanda lise öğrencileri için öğretim yardımcısı olarak da kullanılabilir. Çalışmada önerilen görevler ilginçtir ve çözülmesi her zaman kolay değildir; bu, öğrencilerin eğitimsel motivasyonunu daha bilinçli hale getirmeyi, yeteneklerini test etmeyi ve okul mezunlarının üniversitelere girmeye hazırlık düzeyini artırmayı mümkün kılar. Önerilen alıştırmaların farklı bir seçimi, materyale hakim olmanın üreme düzeyinden yaratıcı olana geçişi ve standart dışı problemleri çözerken bilginizi nasıl uygulayacağınızı öğretme fırsatını içerir.Bölüm 1. Giriş.
Bölüm 1. Mutlak değerin belirlenmesi .
Tanım : Gerçek bir sayının mutlak değeri (modülü) A negatif olmayan bir sayıya denir: A veya -A. Tanım: │ A │ Giriş şu şekildedir: "a sayısının modülü" veya "a sayısının mutlak değeri"│ a, eğer a > 0 ise
│a│ = │ 0, eğer a = 0 (1)
│ - ve eğerÖrnekler: 1) │2,5│ = 2,5 2) │-7│ = 7 3) │1 - √2│ = √2 – 1
- İfade modülünü genişletin:
Bölüm 2. Temel özellikler.
Mutlak değerin temel özelliklerini ele alalım. Mülk #1: Karşıt sayıların eşit modülleri vardır, yani. │а│=│- а│ Eşitliğin doğru olduğunu gösterelim. Sayının tanımını yazalım - A : │- bir│= (2) (1) ve (2) numaralı kümeleri karşılaştıralım. Açıkçası, sayıların mutlak değerlerinin tanımları A Ve - A eşleştir. Buradan, │а│=│- а│Aşağıdaki özellikleri göz önünde bulundururken, kanıtları aşağıda verildiğinden kendimizi onların formülasyonuyla sınırlayacağız. Özellik #2: Sonlu sayıda gerçek sayıların toplamının mutlak değeri, terimlerin mutlak değerlerinin toplamını aşmaz: │а 1 + а 2 +…+ а n │ ≤│а 1 │+│а 2 │ + … + │а n │ Özellik #3: İki reel sayı arasındaki farkın mutlak değeri, mutlak değerlerinin toplamını aşmaz: │а - в│ ≤│а│+│в│ Mülk #4: Sonlu sayıda gerçek sayıların çarpımının mutlak değeri, faktörlerin mutlak değerlerinin çarpımına eşittir: │а·в│=│а│·│в│ Mülk #5: Reel sayıların bölümünün mutlak değeri, mutlak değerlerinin bölümüne eşittir:

Bölüm 3. Bir sayının modülü kavramının geometrik yorumu.
Her gerçek sayı, sayı doğrusu üzerinde bu gerçek sayının geometrik görüntüsü olacak bir noktayla ilişkilendirilebilir. Sayı doğrusu üzerindeki her nokta orijine olan uzaklığına karşılık gelir, yani. segmentin başlangıç noktasından belirli bir noktaya kadar olan uzunluğu. Bu mesafe her zaman negatif olmayan bir değer olarak kabul edilir. Bu nedenle karşılık gelen bölümün uzunluğu, belirli bir gerçek sayının mutlak değerinin geometrik yorumu olacaktır.
Sunulan geometrik çizim, 1 numaralı özelliği açıkça doğrulamaktadır; zıt sayıların modülleri eşittir. Buradan eşitliğin geçerliliği kolaylıkla anlaşılmaktadır: │х – а│= │а – x│. m ≥ 0, yani x 1,2 = ± m olan │х│= m denkleminin çözümü de daha açık hale gelir. Örnekler: 1) │х│= 4 x 1,2 = ± 4 2) │х - 3│= 1
 x 1,2 = 2; 4
x 1,2 = 2; 4 Bölüm 4. y = │х│ fonksiyonunun grafiği
Bu fonksiyonun tanım kümesi tamamen gerçek sayılardır.Bölüm 5. Sözleşmeler.
Gelecekte denklem çözme örnekleri dikkate alınırken aşağıdakiler kullanılacaktır: semboller: ( - sistemin işareti [ - bütünlüğün işareti Bir denklem sistemini (eşitsizlikleri) çözerken, sistemde yer alan denklemlerin (eşitsizliklerin) çözümlerinin kesişimi bulunur. Bir denklem kümesini (eşitsizlikler) çözerken, denklem kümesinde (eşitsizlikler) bulunan çözümlerin birliği bulunur.Bölüm 2. Modül içeren denklemlerin çözümü.
Bu bölümde bir veya daha fazla modül içeren denklemlerin çözümü için cebirsel yöntemlere bakacağız.Bölüm 1. │F(x)│= m formundaki denklemler
Bu tür bir denkleme en basit denir. Yalnızca m ≥ 0 olması durumunda bir çözümü vardır. Modül tanımı gereği, orijinal denklem iki denklemden oluşan bir diziye eşdeğerdir: │ F(x)│=M
 Örnekler:
Örnekler:
№1. Denklemi çözün: │7х - 2│= 9


 Cevap: x 1
= - 1; X 2
= 1
4
/
7
№2
Cevap: x 1
= - 1; X 2
= 1
4
/
7
№2
│x 2 + 3x + 1│= 1

 x 2 + 3x + 2 = 0 x 2 +3x = 0 x 1 = -1; x 2 = -2 x (x + 3) = 0 x 1 = 0; x2 = -3 Cevap: Köklerin toplamı -2.№3
x 2 + 3x + 2 = 0 x 2 +3x = 0 x 1 = -1; x 2 = -2 x (x + 3) = 0 x 1 = 0; x2 = -3 Cevap: Köklerin toplamı -2.№3
│x 4 -5x 2 + 2│= 2 x 4 – 5x 2 = 0 x 4 – 5x 2 + 4 = 0 x 2 (x 2 – 5) = 0, x 2 = m'yi belirtir, m ≥ 0 x = 0 ; ±√5 m 2 – 5 m + 4 = 0 m = 1; 4 – her iki değer de m ≥ 0 x 2 = 1 x 2 = 4 x = ± 1 x = ± 2 koşulunu karşılamaktadır Cevap: Denklemin kök sayısı 7. Egzersizler:
№1. Denklemi çözün ve köklerin toplamını belirtin: │х - 5│= 3 №2 . Denklemi çözün ve daha küçük olan kökü belirtin: │x 2 + x│= 0 №3 . Denklemi çözün ve büyük kökü belirtin: │x 2 – 5x + 4│= 4 №4 .Denklemi çözün ve kökün tamamını belirtin: │2x 2 – 7x + 6│= 1 №5 .Denklemi çözün ve kök sayısını belirtin: │x 4 – 13x 2 + 50│= 14
Bölüm 2. F(│х│) = m formundaki denklemler
Sol taraftaki fonksiyon argümanı modül işaretinin altındadır ve sağ kısım değişkene bağlı değildir. Bu tür denklemleri çözmenin iki yolunu ele alalım. 1 yol: Mutlak değerin tanımı gereği, orijinal denklem iki sistemin birleşimine eşdeğerdir. Her birinde bir alt modüler ifadeye bir koşul uygulanır. F(│x│) =M F(│x│) fonksiyonu tüm tanım kümesi boyunca çift olduğundan, F(x) = m ve F(- x) = m denklemlerinin kökleri zıt sayı çiftleridir. Bu nedenle sistemlerden birini çözmek yeterlidir (örnekler bu şekilde ele alındığında tek sistemin çözümü verilecektir). Yöntem 2: Yeni bir değişken ekleme yönteminin uygulanması. Bu durumda, a ≥ 0 olan │x│= a tanımı eklenir. Bu yöntem tasarım açısından daha az hacimlidir.
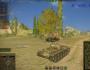
F(│x│) fonksiyonu tüm tanım kümesi boyunca çift olduğundan, F(x) = m ve F(- x) = m denklemlerinin kökleri zıt sayı çiftleridir. Bu nedenle sistemlerden birini çözmek yeterlidir (örnekler bu şekilde ele alındığında tek sistemin çözümü verilecektir). Yöntem 2: Yeni bir değişken ekleme yönteminin uygulanması. Bu durumda, a ≥ 0 olan │x│= a tanımı eklenir. Bu yöntem tasarım açısından daha az hacimlidir. Örnekler: №1 . Denklemi çözün: 3x 2 – 4│x│= - 1 Yeni bir değişkenin tanıtımını kullanalım. a ≥ 0 olmak üzere │x│= a'yı gösterelim. 3a 2 - 4a + 1 = 0 denklemini elde ederiz. D = 16 – 12 = 4 a 1 = 1 a 2 = 1 / 3 Orijinal değişkene dönelim: │ x│=1 ve │х│= 1/3. Her denklemin iki kökü vardır. Cevap: x 1 = 1; X 2 = - 1; X 3 = 1 / 3 ; X 4 = - 1 / 3 . №2. Denklemi çözün: 5x 2 + 3│x│- 1 = 1 / 2 │x│ + 3x 2
 Popülasyonun ilk sisteminin çözümünü bulalım: 4x 2 + 5x – 2 =0 D = 57 x 1 = -5+√57 / 8 x 2 = -5-√57 / 8 x 2'nin sağlamadığına dikkat edin x ≥ 0 koşulu. Çözüm ikinci sistemde x 1 değerinin karşısındaki sayı olacaktır. Cevap: x 1
=
-5+√57
/
8
; X 2
=
5-√57
/
8
.№3
.
Denklemi çözün: x 4 – │х│= 0 │х│= a'yı gösterelim, burada a ≥ 0. a 4 – a = 0 a · (a 3 – 1) = 0 a 1 = 0 denklemini elde ederiz. a 2 = 1 Orijinal değişkene dönün: │х│=0 ve │х│= 1 x = 0; ± 1 Cevap: x 1
= 0; X 2
= 1; X 3
= - 1.
Popülasyonun ilk sisteminin çözümünü bulalım: 4x 2 + 5x – 2 =0 D = 57 x 1 = -5+√57 / 8 x 2 = -5-√57 / 8 x 2'nin sağlamadığına dikkat edin x ≥ 0 koşulu. Çözüm ikinci sistemde x 1 değerinin karşısındaki sayı olacaktır. Cevap: x 1
=
-5+√57
/
8
; X 2
=
5-√57
/
8
.№3
.
Denklemi çözün: x 4 – │х│= 0 │х│= a'yı gösterelim, burada a ≥ 0. a 4 – a = 0 a · (a 3 – 1) = 0 a 1 = 0 denklemini elde ederiz. a 2 = 1 Orijinal değişkene dönün: │х│=0 ve │х│= 1 x = 0; ± 1 Cevap: x 1
= 0; X 2
= 1; X 3
= - 1.
Egzersizler: №6. Denklemi çözün: 2│х│ - 4,5 = 5 – 3 / 8 │х│ №7 . Denklemi çözün, cevabınızdaki kök sayısını belirtin: 3x 2 - 7│x│ + 2 = 0 №8 . Denklemi çözün, cevabınızda tamsayı çözümleri belirtin: x 4 + │x│ - 2 = 0
Bölüm 3. │F(x)│ = G(x) formundaki denklemler
Bu tür bir denklemin sağ tarafı bir değişkene bağlıdır ve bu nedenle ancak ve ancak sağ tarafın bir G(x) ≥ 0 fonksiyonu olması durumunda bir çözümü vardır. Orijinal denklem iki şekilde çözülebilir : 1 yol: Standart, tanımına dayalı bir modülün açıklanmasına dayalı ve iki sistemin birleşimine eşdeğer bir geçişten oluşmaktadır. │ F(x)│ =G(X)
 Bu yöntem, G(x) fonksiyonu için karmaşık bir ifade ve F(x) fonksiyonu için daha az karmaşık bir ifade durumunda rasyonel olarak kullanılabilir, çünkü F(x) fonksiyonu ile eşitsizliklerin çözüleceği varsayılır. Yöntem 2: Sağ tarafa bir koşulun uygulandığı eşdeğer bir sisteme geçişten oluşur. │ F(X)│=
G(X)
Bu yöntem, G(x) fonksiyonu için karmaşık bir ifade ve F(x) fonksiyonu için daha az karmaşık bir ifade durumunda rasyonel olarak kullanılabilir, çünkü F(x) fonksiyonu ile eşitsizliklerin çözüleceği varsayılır. Yöntem 2: Sağ tarafa bir koşulun uygulandığı eşdeğer bir sisteme geçişten oluşur. │ F(X)│=
G(X)

 G(x) fonksiyonuna ilişkin ifade, F(x) fonksiyonuna göre daha az karmaşıksa bu yöntemin kullanılması daha uygundur, çünkü G(x) ≥ 0 eşitsizliğinin çözümü varsayılır. birden fazla modülden ikinci seçeneğin kullanılması önerilir. Örnekler:
№1.
Denklemi çözün: │x + 2│= 6 -2x
G(x) fonksiyonuna ilişkin ifade, F(x) fonksiyonuna göre daha az karmaşıksa bu yöntemin kullanılması daha uygundur, çünkü G(x) ≥ 0 eşitsizliğinin çözümü varsayılır. birden fazla modülden ikinci seçeneğin kullanılması önerilir. Örnekler:
№1.
Denklemi çözün: │x + 2│= 6 -2x  (1 yollu) Cevap: x = 1 1
/
3
№2.
(1 yollu) Cevap: x = 1 1
/
3
№2.
│х 2 – 2х - 1│= 2·(x + 1)
 (2 yol) Cevap: Köklerin çarpımı 3'tür.
(2 yol) Cevap: Köklerin çarpımı 3'tür.№3. Denklemi çözün ve cevabınızdaki köklerin toplamını belirtin:
│x - 6│= x 2 - 5x + 9

Cevap: Köklerin toplamı 4'tür.
Egzersizler: №9. │x + 4│= - 3x №10. Denklemi çözün, cevabınızdaki çözüm sayısını belirtin:│x 2 + x - 1│= 2x – 1 №11 . Denklemi çözün, cevabınızda köklerin çarpımını belirtin:│x + 3│= x 2 + x – 6
Bölüm 4. │F(x)│= F(x) ve │F(x)│= - F(x) formunun denklemleri
Bu tür denklemlere bazen "en güzel" denir. Denklemlerin sağ tarafı değişkene bağlı olduğundan, çözümler ancak ve ancak sağ tarafın negatif olmaması durumunda mevcuttur. Bu nedenle orijinal denklemler eşitsizliklere eşdeğerdir:│F(x)│= F(x) F(x) ≥ 0 ve │F(x)│= - F(x) F(x) Örnekler: №1 . Denklemi çözün, cevabınızdaki tam kökün küçüğünü belirtin: │5x - 3│= 5x – 3 5x – 3 ≥ 0 5x ≥ 3 x ≥ 0,6 Cevap: x = 1№2. Denklemi çözün, aralığın uzunluğunu cevabınızda belirtin: │х 2 - 9│= 9 – x 2 x 2 – 9 ≤ 0 (x – 3) (x + 3) ≤ 0 [- 3; 3] Cevap: Boşluğun uzunluğu 6'dır.№3 . Denklemi çözün ve cevabınızdaki tam sayı çözümlerin sayısını belirtin: │2 + x – x 2 │= 2 + x – x 2 2 + x – x 2 ≥ 0 x 2 – x – 2 ≤ 0 [- 1; 2] Cevap: 4 tam çözüm.№4 . Denklemi çözün ve cevabınızdaki en büyük kökü belirtin:
│4 – x -
 │= 4 – x –
│= 4 – x –  x 2 – 5x + 5 = 0 D = 5 x 1,2 =
x 2 – 5x + 5 = 0 D = 5 x 1,2 =  ≈ 1,4
≈ 1,4Cevap: x = 3.
Egzersizler:
№12.
Denklemi çözün, cevabınızda kökün tamamını belirtin: │x 2 + 6x + 8│= x 2 + 6x + 8 №13.
Denklemi çözün, cevabınızdaki tamsayı çözümlerin sayısını belirtin: │13x – x 2 - 36│+ x 2 – 13x + 36 = 0 №14.
Denklemi çözün; cevabınızda denklemin kökü olmayan bir tamsayıyı belirtin: 
Bölüm 5. │F(x)│= │G(x)│ formundaki denklemler
Denklemin her iki tarafı da negatif olmadığından çözüm iki durumu dikkate almayı gerektirir: alt modüler ifadeler eşit veya zıt işaretlidir. Bu nedenle orijinal denklem iki denklemin birleşimine eşdeğerdir: │ F(X)│= │ G(X)│ Örnekler:
№1.
Denklemi çözün, cevabınızda kökün tamamını belirtin: │x + 3│=│2x - 1│
Örnekler:
№1.
Denklemi çözün, cevabınızda kökün tamamını belirtin: │x + 3│=│2x - 1│  Cevap: Tam kök x = 4.№2.
Denklemi çözün: │
x – x 2 - 1│=│2x – 3 – x 2 │
Cevap: Tam kök x = 4.№2.
Denklemi çözün: │
x – x 2 - 1│=│2x – 3 – x 2 │  Cevap: x = 2.№3
.
Denklemi çözün ve cevabınızda köklerin çarpımını belirtin:
Cevap: x = 2.№3
.
Denklemi çözün ve cevabınızda köklerin çarpımını belirtin: 


 Kök denklemler 4x 2 + 2x – 1 = 0 x 1,2 = - 1±√5 / 4 Cevap: Köklerin çarpımı – 0,25’tir. Egzersizler:
№15
. Denklemi çözün ve cevabınızda çözümün tamamını belirtin: │x 2 – 3x + 2│= │x 2 + 6x - 1│ №16.
Denklemi çözün, cevabınızdaki kökün küçük olanını belirtin:│5x - 3│=│7 - x│ №17
. Denklemi çözün ve cevabınızdaki köklerin toplamını belirtin:
Kök denklemler 4x 2 + 2x – 1 = 0 x 1,2 = - 1±√5 / 4 Cevap: Köklerin çarpımı – 0,25’tir. Egzersizler:
№15
. Denklemi çözün ve cevabınızda çözümün tamamını belirtin: │x 2 – 3x + 2│= │x 2 + 6x - 1│ №16.
Denklemi çözün, cevabınızdaki kökün küçük olanını belirtin:│5x - 3│=│7 - x│ №17
. Denklemi çözün ve cevabınızdaki köklerin toplamını belirtin: 
Bölüm 6. Standart olmayan denklemlerin çözümüne örnekler
Bu bölümde, ifadenin mutlak değerinin tanım gereği ortaya çıktığını çözerken standart olmayan denklem örneklerine bakacağız. Örnekler:№1.
Denklemi çözün, cevabınızdaki köklerin toplamını belirtin: x · │x│- 5x – 6 = 0  Cevap: Köklerin toplamı 1'dir №2.
.
Denklemi çözün, cevabınızdaki kökün küçük olanını belirtin: x 2 - 4x ·
Cevap: Köklerin toplamı 1'dir №2.
.
Denklemi çözün, cevabınızdaki kökün küçük olanını belirtin: x 2 - 4x ·  - 5 = 0
- 5 = 0  Cevap: daha küçük kök x = - 5. №3.
Denklemi çözün:
Cevap: daha küçük kök x = - 5. №3.
Denklemi çözün:  Cevap: x = -1. Egzersizler:
№18.
Denklemi çözün ve köklerin toplamını belirtin: x · │3x + 5│= 3x 2 + 4x + 3
Cevap: x = -1. Egzersizler:
№18.
Denklemi çözün ve köklerin toplamını belirtin: x · │3x + 5│= 3x 2 + 4x + 3
№19.
Denklemi çözün: x 2 – 3x = 
№20.
Denklemi çözün: 
Bölüm 7. │F(x)│+│G(x)│=0 formundaki denklemler
Bu tür denklemin sol tarafında negatif olmayan miktarların toplamının bulunduğunu fark etmek kolaydır. Bu nedenle, orijinal denklemin bir çözümü ancak ve ancak her iki terimin de aynı anda sıfıra eşit olması durumunda vardır. Denklem denklem sistemine eşdeğerdir: │ F(X)│+│ G(X)│=0 Örnekler:
№1
. Denklemi çözün:
Örnekler:
№1
. Denklemi çözün:  Cevap: x = 2. №2.
Denklemi çözün: Cevap: x = 1. Egzersizler:
№21.
Denklemi çözün: №22
. Denklemi çözün ve cevabınızdaki köklerin toplamını belirtin: №23
. Denklemi çözün ve cevabınızdaki çözüm sayısını belirtin:
Cevap: x = 2. №2.
Denklemi çözün: Cevap: x = 1. Egzersizler:
№21.
Denklemi çözün: №22
. Denklemi çözün ve cevabınızdaki köklerin toplamını belirtin: №23
. Denklemi çözün ve cevabınızdaki çözüm sayısını belirtin: Bölüm 8. │a 1 x + b 1 │±│a 2 x + b 2 │± … │a n x +b n │= m formundaki denklemler
Bu tür denklemleri çözmek için aralık yöntemi kullanılır. Bunu modüllerin sıralı genişletilmesiyle çözersek, şunu elde ederiz: Nçok hantal ve elverişsiz olan sistem setleri. Aralık yöntemi algoritmasını ele alalım: 1). Değişken değerlerini bulun X, her modülün sıfıra eşit olduğu (alt modüler ifadelerin sıfırları): 2). Bulunan değerleri aralıklara bölünmüş bir sayı doğrusu üzerinde işaretleyin (aralık sayısı sırasıyla eşittir) N+1
) 3). Elde edilen aralıkların her birinde her modülün hangi işaretle ortaya çıktığını belirleyin (çözüm yaparken, üzerindeki işaretleri işaretleyerek bir sayı doğrusu kullanabilirsiniz) 4). Orijinal denklem toplama eşdeğerdir N+1
Her birinde değişkenin üyeliğinin belirtildiği sistemler X aralıklardan biridir. Örnekler:
№1
. Denklemi çözün ve cevabınızdaki en büyük kökü belirtin:
2). Bulunan değerleri aralıklara bölünmüş bir sayı doğrusu üzerinde işaretleyin (aralık sayısı sırasıyla eşittir) N+1
) 3). Elde edilen aralıkların her birinde her modülün hangi işaretle ortaya çıktığını belirleyin (çözüm yaparken, üzerindeki işaretleri işaretleyerek bir sayı doğrusu kullanabilirsiniz) 4). Orijinal denklem toplama eşdeğerdir N+1
Her birinde değişkenin üyeliğinin belirtildiği sistemler X aralıklardan biridir. Örnekler:
№1
. Denklemi çözün ve cevabınızdaki en büyük kökü belirtin:  1). Alt modüler ifadelerin sıfırlarını bulalım: x = 2; x = -3 2). Bulunan değerleri sayı doğrusu üzerinde işaretleyelim ve ortaya çıkan aralıklarda her modülün hangi işaretle ortaya çıktığını belirleyelim:
1). Alt modüler ifadelerin sıfırlarını bulalım: x = 2; x = -3 2). Bulunan değerleri sayı doğrusu üzerinde işaretleyelim ve ortaya çıkan aralıklarda her modülün hangi işaretle ortaya çıktığını belirleyelim: x – 2 x – 2 x – 2 - - + - 3 2x2x + 6 2x + 6 2x + 6 - + + 3)
 - çözüm yok Denklemin iki kökü var. Cevap: En büyük kök x = 2. №2.
Denklemi çözün ve cevabınızda kökün tamamını belirtin:
- çözüm yok Denklemin iki kökü var. Cevap: En büyük kök x = 2. №2.
Denklemi çözün ve cevabınızda kökün tamamını belirtin:  1). Alt modüler ifadelerin sıfırlarını bulalım: x = 1,5; x = - 1 2). Bulunan değerleri sayı doğrusu üzerinde işaretleyelim ve ortaya çıkan aralıklarda her modülün hangi işaretle ortaya çıktığını belirleyelim: x + 1 x + 1 x + 1 - + +
1). Alt modüler ifadelerin sıfırlarını bulalım: x = 1,5; x = - 1 2). Bulunan değerleri sayı doğrusu üzerinde işaretleyelim ve ortaya çıkan aralıklarda her modülün hangi işaretle ortaya çıktığını belirleyelim: x + 1 x + 1 x + 1 - + + -1 1,5 x 2x – 3 2x – 3 2x – 3 - - +
3).
 Son sistemin çözümü yoktur, dolayısıyla denklemin iki kökü vardır. Denklemi çözerken ikinci modülün önündeki “-” işaretine dikkat etmelisiniz. Cevap: Tam kök x = 7. №3.
Denklemi çözün, cevabınızda köklerin toplamını belirtin: 1). Alt modüler ifadelerin sıfırlarını bulalım: x = 5; x = 1; x = - 2 2). Bulunan değerleri sayı doğrusu üzerinde işaretleyelim ve ortaya çıkan aralıklarda her modülün hangi işaretle ortaya çıktığını belirleyelim: x – 5 x – 5 x – 5 x – 5 - - - +
Son sistemin çözümü yoktur, dolayısıyla denklemin iki kökü vardır. Denklemi çözerken ikinci modülün önündeki “-” işaretine dikkat etmelisiniz. Cevap: Tam kök x = 7. №3.
Denklemi çözün, cevabınızda köklerin toplamını belirtin: 1). Alt modüler ifadelerin sıfırlarını bulalım: x = 5; x = 1; x = - 2 2). Bulunan değerleri sayı doğrusu üzerinde işaretleyelim ve ortaya çıkan aralıklarda her modülün hangi işaretle ortaya çıktığını belirleyelim: x – 5 x – 5 x – 5 x – 5 - - - + -2 1 5 x x – 1 x – 1 x – 1 x – 1 - - + + x + 2 x + 2 x + 2 x + 2 - + + +
3).
 Denklemin x = 0 ve 2 olmak üzere iki kökü vardır. Cevap: Köklerin toplamı 2'dir. №4
.
Denklemi çözün: 1). Alt modüler ifadelerin sıfırlarını bulalım: x = 1; x = 2; x = 3.2). Ortaya çıkan aralıklarda her modülün hangi işaretle ortaya çıktığını belirleyelim. 3).
Denklemin x = 0 ve 2 olmak üzere iki kökü vardır. Cevap: Köklerin toplamı 2'dir. №4
.
Denklemi çözün: 1). Alt modüler ifadelerin sıfırlarını bulalım: x = 1; x = 2; x = 3.2). Ortaya çıkan aralıklarda her modülün hangi işaretle ortaya çıktığını belirleyelim. 3).  İlk üç sistemin çözümlerini birleştirelim. Cevap: ; x = 5.
İlk üç sistemin çözümlerini birleştirelim. Cevap: ; x = 5.Egzersizler: №24. Denklemi çözün:
 №25.
Denklemi çözün ve cevabınızdaki köklerin toplamını belirtin: №26.
Denklemi çözün ve cevabınızdaki daha küçük kökü belirtin: №27.
Denklemi çözün ve cevabınızdaki büyük kökü belirtin:
№25.
Denklemi çözün ve cevabınızdaki köklerin toplamını belirtin: №26.
Denklemi çözün ve cevabınızdaki daha küçük kökü belirtin: №27.
Denklemi çözün ve cevabınızdaki büyük kökü belirtin: Bölüm 9. Birkaç modül içeren denklemler
Birden fazla modül içeren denklemler, alt modüler ifadelerde mutlak değerlerin varlığını varsayar. Bu tür denklemleri çözmenin temel ilkesi, modüllerin “harici” olandan başlayarak sıralı olarak açıklanmasıdır. Çözüm sırasında 1 No'lu Bölüm 3'te anlatılan teknikler kullanılır.Örnekler:
№1.
Denklemi çözün:  Cevap: x = 1; - on bir. №2.
Denklemi çözün:
Cevap: x = 1; - on bir. №2.
Denklemi çözün:
Cevap: x = 0; 4; - 4. №3.
Denklemi çözün ve cevabınızda köklerin çarpımını belirtin:  Cevap: Köklerin çarpımı -8'dir. №4.
Denklemi çözün:
Cevap: Köklerin çarpımı -8'dir. №4.
Denklemi çözün:  Nüfus denklemlerini gösterelim (1)
Ve (2)
ve tasarım kolaylığı için her birinin çözümünü ayrı ayrı düşünün. Her iki denklem de birden fazla modül içerdiğinden sistem kümelerine eşdeğer bir geçiş yapmak daha uygundur. (1)
Nüfus denklemlerini gösterelim (1)
Ve (2)
ve tasarım kolaylığı için her birinin çözümünü ayrı ayrı düşünün. Her iki denklem de birden fazla modül içerdiğinden sistem kümelerine eşdeğer bir geçiş yapmak daha uygundur. (1)

 (2)
(2)


 Cevap:
Cevap:
Egzersizler:
№36.
Denklemi çözün, cevabınızdaki köklerin toplamını belirtin: 5 │3x-5│ = 25 x №37.
Denklemi çözün, birden fazla kök varsa cevabınızda köklerin toplamını belirtin: │x + 2│ x – 3x – 10 = 1 №38.
Denklemi çözün: 3 │2x -4│ = 9 │x│ №39.
Denklemi çözün ve cevabınızdaki kök sayısını belirtin: 2 │ sin x│ = √2 №40
. Denklemi çözün ve cevabınızdaki kök sayısını belirtin:
Bölüm 3. Logaritmik denklemler.
Aşağıdaki denklemleri çözmeden önce logaritmanın ve logaritmik fonksiyonun özelliklerini gözden geçirmek gerekir. Örnekler: №1. Denklemi çözün, cevabınızda köklerin çarpımını belirtin: log 2 (x+1) 2 + log 2 │x+1│ = 6 O.D.Z. x+1≠0 x≠ - 1Durum 1: x ≥ - 1 ise log 2 (x+1) 2 + log 2 (x+1) = 6 log 2 (x+1) 3 = log 2 2 6 (x+1) 3 = 2 6 x+1 = 4 x = 3 – x ≥ - 1 koşulunu karşılar 2 durum: eğer x log 2 (x+1) 2 + log 2 (-x-1) = 6 log 2 (x+1) 2 + log 2 (-(x+1)) = 6 log 2 (-(x+1) 3) = log 2 2 6- (x+1) 3 = 2 6- (x+1) = 4 x = - 5 – x - 1 koşulunu karşılıyor
Cevap: Köklerin çarpımı – 15’tir.
№2.
Denklemi çözün, cevabınızdaki köklerin toplamını belirtin: lg  O.D.Z.
O.D.Z. 



Cevap: Köklerin toplamı 0,5'tir.
№3.
Denklemi çözün: log 5  O.D.Z.
O.D.Z. 
 Cevap: x = 9. №4.
Denklemi çözün: │2 + log 0,2 x│+ 3 = │1 + log 5 x│ O.D.Z. x > 0 Başka bir tabana geçmek için formülü kullanalım. │2 - log 5 x│+ 3 = │1 + log 5 x│
Cevap: x = 9. №4.
Denklemi çözün: │2 + log 0,2 x│+ 3 = │1 + log 5 x│ O.D.Z. x > 0 Başka bir tabana geçmek için formülü kullanalım. │2 - log 5 x│+ 3 = │1 + log 5 x│
│2 - log 5 x│- │1 + log 5 x│= - 3 Alt modüler ifadelerin sıfırlarını bulalım: x = 25; x = Bu sayılar kabul edilebilir değer aralığını üç aralığa böler, dolayısıyla denklem üç sistemden oluşan bir kümeye eşdeğerdir.  Cevap: )
Cevap: )